Question
Question: A coil of radius \(R\) carries current \({i_1}\). Another concentric coil of radius \[r(r \ll R)\] c...
A coil of radius R carries current i1. Another concentric coil of radius r(r≪R) carries current i2. Places of two coils are mutually perpendicular and both the coils are free to rotate about common diameter. If the maximum kinetic energy of smaller coil when both are released is X(MR2+mr2)μ0i1i2πr2MR. Find X?
Masses of coils are M and m, respectively.
Solution
To solve this question think about the conservation of the angular momentum. By finding the inertia, angular velocity, potential energy we are able to find the solution for this question.
Formula used:
I1ω1 = I2ω2
21I1ω12+21I2ω22=U
U=MBcosθ
Complete step by step answer:
We can find the solutions by understanding the laws of conservation of angular momentum and energy.
The law of conservation of energy states that the energy can be neither created nor can it be destroyed.
Given that a coil of radius R carries current i1 and another concentric coil of radius r(r≪R) carries current i2. The Mass of the coil with radius R is M and mass of the coil with radius r is m.
Also, places of two coils are mutually perpendicular and both the coils are free to rotate about common diameter as shown in the diagram.
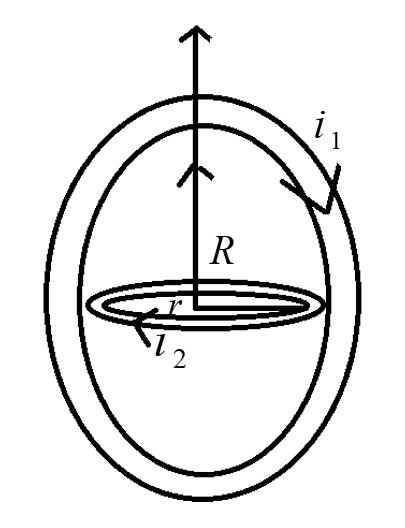
The magnetic induction at centre due to current in larger coil, B=2Rμ0i1μ∘
Where
B is the magnetic induction.
μ∘is the permeability of free space.
R is the radius
Also, magnetic moment is given as M=I×A
Where,
M is the magnetic moment
I is the current
Hence for smaller coil magnetic moment M=πr2i2
Initially when the coils are perpendicular to each other the angle between M and B is 90∘ hence potential energy is given as
U1=−MBcos90∘=0
When the coils become coplanar the angle between M and B is 0∘ hence potential energy U2 is given as
U2=−MBcos0∘=−MB
Therefore, decrease in the potential energy, U=U1−U2
⇒U=0−(−MB)
⇒U=MB=2Rμ0i1i2πr2
This decrease in potential energy is converted into kinetic energy.
Also, kinetic energy becomes maximum when the coils are coplanar.
Let ω1 and ω2be angular velocity and I1 I2 be the moment of inertia of larger and smaller coil respectively when the coils become coplanar.
Also I1=MR2and I2=mr2
According to law of conservation of angular momentum I1ω1 = I2ω2
Hence we have ω1=I1I2ω2
Also, kinetic energy of rotating body is given as 21Iω2
Hence, according to law of conservation of energy,
⇒21I1ω12+21I2ω22=U
Using the value ω1=I1I2ω2
We have,
⇒21I1(I1I2ω2)2+21I2ω22=U
⇒U=21I1ω22(I2I1+1)
⇒21I1ω22=I1+I2UI1
By substituting the values for U, I1 and I2 we get,
⇒21I1ω22=2(MR2+mr2)μoi1i2πr2MR
Where kinetic energy is 21I1ω22
By comparing the equations X(MR2+mr2)μ0i1i2πr2MR and 2(MR2+mr2)μoi1i2πr2MR we get X=2
Therefore X=2 is the required answer.
Note:
The law of conservation of angular momentum states that there will be no change in the angular momentum that occurs if no external torque is acting on it. The negative sign in the potential energy U indicates that both the coils are moving in the direction opposite to each other.
