Question

A coil of inductive reactance 31 has a resistance of 8. It is placed in series with a condenser of capacitive reactance 25. The combination is connected to an alternative current source of 110 V. What is the power factor of the circuit?
${\text{A}}{\text{.}}$ 0.64
${\text{B}}{\text{.}}$ 0.75
${\text{C}}{\text{.}}$ 0.80
${\text{D}}{\text{.}}$ 0.56

Answer 1

Hint- Here, we will proceed by finding the net impedance in the given series circuit of given resistance, given inductive and capacitive reactance. Then, we will draw the impedance triangle in order to find the power factor (i.e., $\cos \phi$) for the given circuit.

Formulas Used- ${\text{Z}} = \sqrt {{{\text{R}}^2} + {{\left( {{{\text{X}}_{\text{L}}} - {{\text{X}}_{\text{C}}}} \right)}^2}}$ and $\cos \phi = \dfrac{{\text{R}}}{{\text{Z}}}$.

Complete step-by-step solution -

__

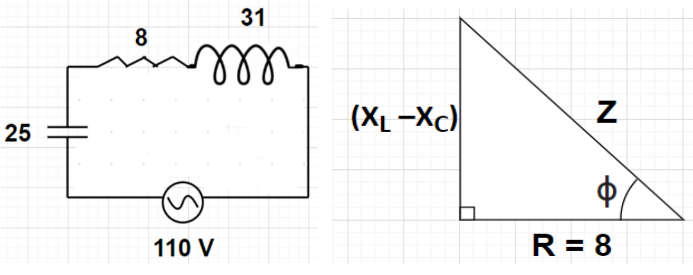
Given, Inductive reactance of the coil, ${{\text{X}}_{\text{L}}}$ = 31 $\Omega$
Resistance of the coil, R = 8 $\Omega$
Capacitive reactance of condenser, ${{\text{X}}_{\text{C}}}$ = 25 $\Omega$
Voltage of the alternative current source, V = 110 volts
It is given that both the coil and the condenser are connected in series with each other.
Since, we know that the net impedance Z of the circuit having resistance R, inductive reactance $X_L$ and capacitive reactance $X_C$ all connected in series is given by
${\text{Z}} = \sqrt {{{\text{R}}^2} + {{\left( {{{\text{X}}_{\text{L}}} - {{\text{X}}_{\text{C}}}} \right)}^2}}$
By substituting${{\text{X}}_{\text{L}}}$ = 31, ${{\text{X}}_{\text{C}}}$ = 25 and V = 110 in the above formula, we get
Impedance of the circuit, ${\text{Z}} = \sqrt {{{\text{8}}^2} + {{\left( {31 - 25} \right)}^2}} = \sqrt {64 + 36} = \sqrt {100} = 10{\text{ }}\Omega$
Power factor of any circuit can be given by $\cos \phi$ where angle $\phi$ is shown in the figure of the impedance triangle drawn.
According to the impedance triangle shown in the figure, we can write
$\cos \phi = \dfrac{{\text{R}}}{{\text{Z}}}$
By substituting R = 8 and Z = 10 in the above equation, we have
$\Rightarrow \cos \phi = \dfrac{{\text{8}}}{{{\text{10}}}} \\\ \Rightarrow \cos \phi = {\text{0}}{\text{.80}} \\\$
Therefore, the power factor of the given circuit is equal to 0.80.
Hence, option C is correct.

Note- According to Pythagoras Theorem, ${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}$. By applying Pythagoras Theorem in the impedance triangle, we get ${\left( {\text{Z}} \right)^2} = {\left( {{{\text{X}}_{\text{L}}} - {{\text{X}}_{\text{C}}}} \right)^2} + {\left( {\text{R}} \right)^2} \Rightarrow {\text{Z}} = \sqrt {{{\left( {{{\text{X}}_{\text{L}}} - {{\text{X}}_{\text{C}}}} \right)}^2} + {{\left( {\text{R}} \right)}^2}}$ which is the same formula as used directly in the problem. Here, ${{\text{X}}_{\text{C}}} < {{\text{X}}_{\text{L}}}$ that’s why everywhere we have used $\left( {{{\text{X}}_{\text{L}}} - {{\text{X}}_{\text{C}}}} \right)$ but for ${{\text{X}}_{\text{C}}} > {{\text{X}}_{\text{L}}}$, we use $\left( {{{\text{X}}_{\text{C}}} - {{\text{X}}_{\text{L}}}} \right)$ instead of $\left( {{{\text{X}}_{\text{L}}} - {{\text{X}}_{\text{C}}}} \right)$.