Question

A coil of inductance 8.4 mH and resistance $6\Omega$is connected to a 12 V battery. The current in the coil is 1 A at approximately the time:
A. 500 s
B. 20 s
C. 35 ms
D. 1 ms

Answer 1

The formula that relates the parameters of electrical components such as, the inductance, the resistance, the emf of a battery and the flow of current should be used to solve this problem. As the values of all the parameters are given, substituting the same, we will compute the value of time taken.
Formula used:
$I={{I}_{0}}\left( 1-{{e}^{-\left( \dfrac{Rt}{L} \right)}} \right)$

Complete answer:
From the given information, we have the data as follows.
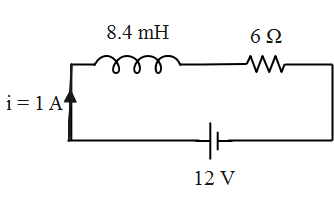
A coil of inductance 8.4 mH and resistance $6\Omega$is connected to a 12 V battery. The current in the coil is 1 A.
$L=8.4\,mH$
$R=6\Omega$
$V=12\,V$
$I=1A$
The circuit diagram representing the same is given as follows.

The formula to solve this problem is the formula for computing the current in the discharging LR circuit. This formula gives the relation between the inductance, the resistance, the emf of a battery and the flow of current.
$I={{I}_{0}}\left( 1-{{e}^{-\left( \dfrac{Rt}{L} \right)}} \right)$
Where ${{I}_{0}}$is the peak current, R is the resistance, t is the time taken and L is the inductance.
Here, the value of current is, ${{I}_{0}}=\dfrac{V}{R}$. Substitute this expression in the above equation.
$I=\dfrac{V}{R}\left( 1-{{e}^{-\left( \dfrac{Rt}{L} \right)}} \right)$
Where V is the voltage and R is the resistance.
Substitute the given values in the above equation.
$1=\dfrac{12}{6}\left( 1-{{e}^{-\left( \dfrac{6\times t}{8.4\times {{10}^{-3}}} \right)}} \right)$
Continue further computation.

& {{e}^{-\left( \dfrac{6\times t}{8.4\times {{10}^{-3}}} \right)}}=1-\dfrac{1}{2} \\\ & \Rightarrow -\left( \dfrac{6\times t}{8.4\times {{10}^{-3}}} \right)=\ln \dfrac{1}{2} \\\ & \Rightarrow \dfrac{6\times t}{8.4\times {{10}^{-3}}}=0.693 \\\ \end{aligned}$$ Rearrange the terms of the above equation to represent the equation in terms of time. $$\begin{aligned} & t=\dfrac{0.693\times 8.4\times {{10}^{-3}}}{6} \\\ & \Rightarrow t=9.702\times {{10}^{-4}} \\\ & \therefore t\approx 1\,ms \\\ \end{aligned}$$ $$\therefore $$ The current in the coil is 1 A at approximately the time is 1 ms. **Thus, option (D) is correct.** **Note:** The current in the discharging LR circuit formula can also be used to solve this problem. The further reduction of this formula leads to the formula that we have used in the explanation to solve this problem.