Question

A coil in the shape of an equilateral triangle of side l is suspended between 2 pole pieces of a permanent magnet such that B is in the plane of the coil. If due to current i in the triangle, a torque$\tau$acts on it. The side l of the triangle is
$A.\quad \dfrac{2}{\sqrt{3}}(\dfrac{\tau }{Bi})$
$B.\quad 2{{(\dfrac{\tau }{\sqrt{3}Bi})}^{\dfrac{1}{2}}}$
$C.\quad \dfrac{2}{\sqrt{3}}{{(\dfrac{\tau }{Bi})}^{\dfrac{1}{2}}}$
$D.\quad \dfrac{1}{\sqrt{3}}\dfrac{\tau }{Bi}$

Answer 1

Hint : Here the knowledge to magnetostatics is required to solve this problem. The right hand rule to find the direction of magnetic field around a current carrying conductor is required. The magnetic moment acting on the coil’s loop is given by, $\vec{\mu }=i\vec{A}$ and the torque $(\tau )$ acting on the coil is given by, $\vec{\tau }=\vec{\mu }\times \vec{B}$ hence, $\tau =iAB.$ Taking the area of the triangle, which is $A=\dfrac{\sqrt{3}}{4}{{l}^{2}}$ needs to substituted in to find the final value of the length of triangle (l).

Complete step by step solution :
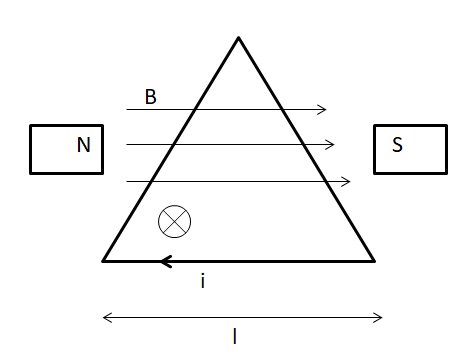
Let’s start off by making a diagram of the problem. We have a coil in the shape of an equilateral triangle in between the pole pieces marked as (N) for North pole magnetic piece and (S) for the South pole magnetic piece. The magnetic field lines are shown, being emitted from N and travelling towards S. The current (i) in the coil is assumed to be flowing in clockwise direction. The length of each side of the equilateral triangle is l. The strength of the magnetic field due to the magnetic poles is B.

The magnetic moment acting on the coil’s loop is given by, $\vec{\mu }=i\vec{A},$ where A refers to the area of the loop of the equilateral triangle.
The direction of the magnetic moment can be found using the Right hand rule, if you consider you are holding the wire, with your thumb pointing towards the direction of the flow of current and the rest of your fingers curl around the wire. Then the direction of the magnetic field produced will be along the direction of the curling fingers. In this case, the magnetic moment as well. Hence, the direction of the magnetic moment is into the plane as shown in the figure.
We also know that the torque $(\tau )$ acting on the coil is given by, $\vec{\tau }=\vec{\mu }\times \vec{B}$ .
As we can see in the figure, the magnetic lines of force are along the plane of the coil and the magnetic moment is into the plane of the coil. Hence, they are perpendicular to each other.
Therefore, $\vec{\tau }=\vec{\mu }\times \vec{B}\Rightarrow \tau =\mu B\sin \theta \Rightarrow \tau =\mu B\sin {{90}^{0}}$ . That is, $\tau =\mu B$ .
Substituting in the value of magnetic moment from above into the value of torque, we get, $\tau =iAB.$
Therefore, $A=\dfrac{\tau }{iB}.$ For an equilateral triangle of side length l, the area of the triangle will be $A=\dfrac{\sqrt{3}}{4}{{l}^{2}}.$ Hence, $A=\dfrac{\sqrt{3}}{4}{{l}^{2}}=\dfrac{\tau }{iB}\Rightarrow {{l}^{2}}=\dfrac{4\tau }{\sqrt{3}iB}\Rightarrow l=2{{(\dfrac{\tau }{\sqrt{3}iB})}^{\dfrac{1}{2}}}$

Note : Here, we’ve considered the number of loops in the coil to be 1.
The Area vector is always outward normal. That is, in this case, the area vector is perpendicular to the plane of the triangle. That is, into or outside the plane. Hence, to find the magnetic moment direction, even when you don’t know the right hand rule, since $\vec{\mu }=i\vec{A},$ $\vec{\mu }$ will take the direction of Area vector. Hence, it’ll eventually be perpendicular to the plane.
To find the area of an equilateral triangle, the basic formula is: Area is equal to half time base time height. Here, let’s drop a perpendicular from the top vertex to the center of the base.

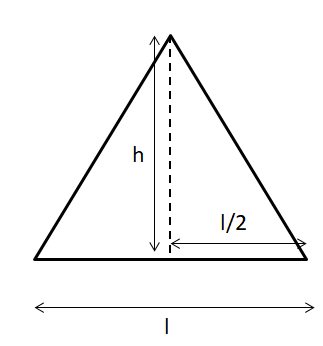
Using the Pythagoras theorem, taking the hypotenuse as l, we have, ${{l}^{2}}={{(\dfrac{l}{2})}^{2}}+{{h}^{2}}\Rightarrow {{h}^{2}}={{l}^{2}}-{{\dfrac{l}{4}}^{2}}\Rightarrow {{h}^{2}}={{l}^{2}}-{{\dfrac{l}{4}}^{2}}\Rightarrow {{h}^{2}}={{\dfrac{3l}{4}}^{2}}\Rightarrow h=\dfrac{\sqrt{3}l}{2}.$
Hence, taking the height of the triangle as $\dfrac{\sqrt{3}l}{2}$ and the base length as l, we get the area to be, $A=\dfrac{1}{2}\times base\times height\Rightarrow A=\dfrac{1}{2}(l)(\dfrac{\sqrt{3}l}{2})\Rightarrow A=\dfrac{\sqrt{3}l}{4}.$