Question

A cockroach is moving with velocity $v$ in anticlockwise direction on the rim of a disc of radius R and mass m. The moment of Inertia of the disc is $I$, and it is rotating in clockwise direction with an angular velocity $\omega$. If the cockroach stops, the angular velocity of disc will be
(a) $\dfrac{{I\omega }}{{I + m{R^2}}}$
(b) $\dfrac{{I\omega + mvr}}{{I + m{R^2}}}$
(c) $\dfrac{{I\omega - mvr}}{{I + m{R^2}}}$
(d) $\dfrac{{I\omega - mvr}}{I}$

Answer 1

Conservation of angular momentum can be used to derive final angular velocity. Since no net external force acts on the combined system moving cockroach and disc.

Formula Used:
Moment of Inertia of particle of mass m(cockroach) rotating at distance R from axis of rotation: $I = m{R^2}$ …… (A)
Angular momentum moving with linear velocity $v$, at a radial distance $R$ from center of rotation : ${L_{cockroach}} = R \times p = R \times mv$ …… (B)
Where, p is linear momentum of particle (this case cockroach)
Angular momentum of body with angular velocity $\omega$ and moment of Inertia $I$:
${L_{disc}} = I\omega$ …… (C)
Conservation of Angular Momentum: When net external force on the system is 0 or line of external force passes through axis of rotation.
Then, $\sum {{L_i} = } \sum {{L_f}}$ …… (D)
Where ${L_i}$ and ${L_f}$ are initial and final momentum respectively.

Complete step by step answer:
Given,
Moment of Inertia of disc $I$, radius of disc = $R$ and angular speed =$\omega$
Mass of cockroach $m$ and
Step 1:
Consider on the clockwise direction of rotation to be positive (for sign convection we can take anticlockwise to be positive as well but for simplicity taken clockwise to be positive)
Diagram: depicting the situation of the problem

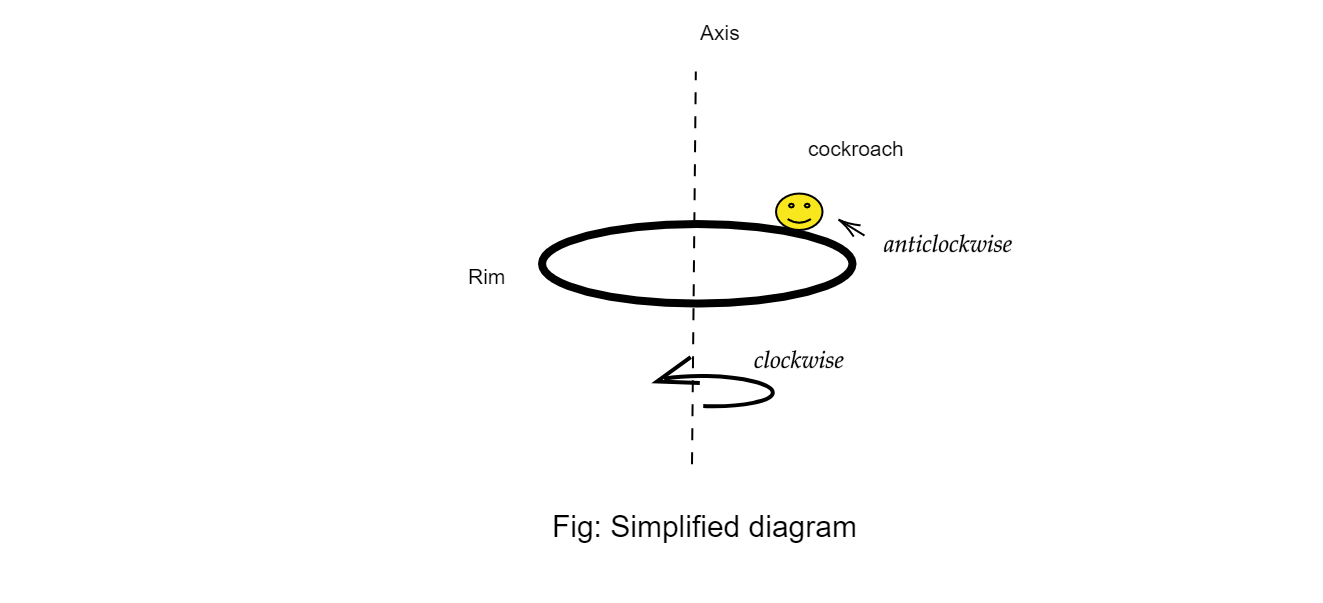
Step 2:
Initial total angular momentum= Angular momentum of moving cockroach +Angular momentum due to rotating disc.
Putting values from equation (B) and (C), we can say
$\Rightarrow \sum {{L_i}} = {L_{cockroach}} + {L_{disc}} = ( - )R \times mv + I\omega$
$\Rightarrow \sum {{L_i}} = - Rmv + I\omega = I\omega - mvR$ …… (1)
Step 3:
Now, when cockroach stopped on the rim. Then it will also move with the rim as it sticks to it.
So, total final moment of inertia of system =${I_{final}} = {I_{disc}} + {I_{cockroach}}$
${I_{final}} = I + m{R^2}$ …… (2)
Step 4:
Let’s say final angular velocity be ${\omega _f}$
Final total angular momentum =$\sum {L{ _f}} = {I_{final}}{\omega _{final}}$
$\sum {L{ _f}} = (I + m{R^2}){\omega _{final}}$ …… (3)
Step 5:
Using conservation of angular momentum as no external force acting in the system:
Putting values from (3) and (2) in equation (D) we get,
$\Rightarrow I\omega - mvR = (I + m{R^2}){\omega _f} \\\ \Rightarrow {\omega _f} = \dfrac{{I\omega - mvR}}{{I + m{R^2}}} \\\$

Therefore, the correct option is (C) $\dfrac{{I\omega - mvr}}{{I + m{R^2}}}$

Note:
Conservation of angular momentum is applicable when it meets the following conditions:
External force on the combined system =0
If the net force isn’t 0, but if the line of force passes through the axis of rotation then again angular momentum is conserved.