Question

A closely wound solenoid of $2000$ turns and area of cross section $1.6\times {{10}^{-4}}{{m}^{2}}$, carrying a current of $4.0A$, is suspended through its centre allowing it to turn in a horizontal plane.
(a) What is the magnetic moment which is associated with the above mentioned solenoid?
(b) What is the force and torque on the solenoid if a uniform horizontal magnetic field of $7.5\times {{10}^{-2}}T$ is set up at an angle of $30{}^\circ$ with the axis of the solenoid?

Answer 1

First of all find out the magnetic moment of the solenoid by substituting the values given in the question. Find its direction using the right hand screw rule. Then find out the torque acting as well as the force acting on the coil due to the uniform magnetic field. Find its direction also. While finding out the force, remember that the magnetic field is given as uniform.

Formula used:
$M=NIA$
Where the magnetic moment is the product of the number of turns, current passing through the coil and the area of cross section.
$\overrightarrow{\tau }=MB\sin \theta$
Where the torque acting is the cross product of the magnetic moment and the magnetic field.

Complete answer:

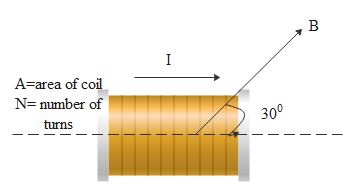
Firstly let us mention the terms given in the question,
The number of turns in the coil is given as,
$N=2000$
Area of the cross section of the solenoid is given as,
$A=1.6\times {{10}^{-4}}{{m}^{2}}$
The current passing through the coil is,
$I=4A$
And also, the magnetic field experienced over there is,
$B=7.5\times {{10}^{-2}}T$
The angle between the solenoid and the magnetic field is given as,
$\theta =30{}^\circ$

(a) The magnetic moment acting on the solenoid is given by the equation,
$\begin{aligned} & M=NIA \\\ & =2000\times 4\times 1.6\times {{10}^{-4}} \\\ & M=1.28A{{m}^{2}} \\\ \end{aligned}$

(b)The force acting over the solenoid will be equal to zero, as the magnetic field is given as uniform. Therefore we can write that,
$F=0N$
The torque acting on the solenoid is given by the equation,
$\overrightarrow{\tau }=MB\sin \theta$
Substituting the values in it will give,

& \overrightarrow{\tau }=MB\sin \theta \\\ & \overrightarrow{\tau }=1.28\times 7.5\times 1{{0}^{-2}}\times \dfrac{1}{2}J \\\ & \overrightarrow{\tau }=0.048J \\\ \end{aligned}$$ **Note:** Using the right hand screw rule, we can find out the direction of the magnetic moment which is along the axis of the solenoid itself. The direction of the torque will be like the solenoid tries to align the axis of the solenoid or the direction of magnetic moment vector, along the direction of the magnetic field $$B$$.