Question

A closed rectangular tank is completely filled with water and is accelerated horizontally with an acceleration towards the right. Pressure is (i) maximum at, and (ii) minimum at

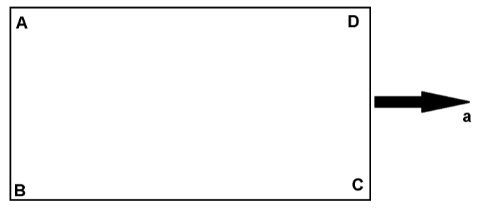
A. (i)B (ii)D
B. (i)C (ii)D
C. (i)B (ii)C
D. (i)B (ii)A

Answer 1

Here it is given that the tank is completely filled with water and is accelerated horizontally, and we must find that at what point pressure will be minimum and maximum. Here we will get the answer by using the basic formula of pressure in fluid let us see.

Formula used:
$P = \rho gh$
Where, $P$ is the pressure, $\rho$ is the density of the fluid, $g$ is the acceleration of gravity and $h$ is the height of the fluid.

Complete step by step answer:
Let, $h$ be the distance between $A$ and $B$. $l$ be the distance between $A$ and $D$.Now, we know that the pressure increases in vertical direction by $\rho gh$.So, the pressure at $B$ will be,
${P_B} = {P_A} + \rho gh$ ----(1)
Pressure at $C$ will be,
${P_C} = {P_D} + \rho gh$

And we know that when any body accelerates in the opposite direction, we experience pressure and are given by, $\rho al$.So, pressure at $A$ will be,
${P_A} = {P_D} + \rho al$
And Pressure at $B$ will be,
${P_B} = {P_C} + \rho al$
Putting value of pressure of $A$ in equation (1) we get,
${P_B} = {P_D} + \rho gh + \rho al$
Here we see that after adding the pressure of $D$ only there is something in all the points so we can conclude that the minimum pressure at $D$.And after adding ${P_D} + \rho gh$ on $B$ only we get the pressure of $B$ so we can say that the pressure at $B$ is the maximum.

Hence, the correct option is A.

Note: Pascal's law (also Pascal's principle or the principle of transmission of fluid-pressure) is a principle in fluid mechanics given by Blaise Pascal that states that a pressure change at any point in a confined incompressible fluid is transmitted throughout the fluid such that the same change occurs everywhere.