Question

A closed gas cylinder is divided into two parts by a piston held tight. The pressure and volume of gas in two parts respectively are (P,5V) and (10P, V). If now the piston is left free and the system undergoes an isothermal process, then the volumes of the gas in two parts respectively are.
A) 2V,4V
B) 3V,3V
C) 5V, V
D) $\dfrac{{10}}{{11}}V,\dfrac{{20}}{{11}}V$

Answer 1

According to the question the system undergoes an isothermal process in this process we have to keep in mind the temperature remains constant. For this question use the Ideal gas equation and keep ‘T’ (temperature) constant due to isothermal process. So, pressure and volume remain constant.
Formula used:
PV= nRT
${P_1}{V_1} = {P_2}{V_2}$

Complete answer:
The question clearly said a closed gas cylinder is divided into two parts by a piston as shown in the figure for better understanding.

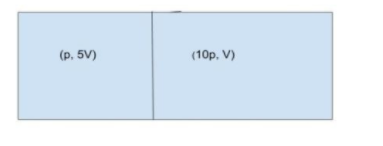
Given, pressure and volume of the gas in the two parts of the cylinder are (p, 5V) and (10p, V).
As given in the question the piston is left free and the system undergoes an isothermal process. We know that in an isothermal process the temperature remains constant.
So, ideal gas equation
PV= nRT
P is the pressure
V is the volume
n is the number of mole
R is the universal gas constant
T is temperature i.e constant
PV= constant
Let, pressure and volume of the gas in the first part is ${P_1}{V_1}$ as given in the question (p, 5V).
And pressure and volume of the gas in the second part ${P_2}{V_2}$ as given in the question (10p, V).
Now, the piston is left free the piston will move towards the lower pressure part till the pressure becomes equal on both parts.
Consider common pressure p. We know that PV= constant So, ${P_1}{V_1} + {P_2}{V_2} = pV$-----(1)${P_1} = p,$${P_2} = 10p$${V_1} = 5V,{V_2} = V$p` is the common pressure V is the total volume$V = {V_1} + {V_2} = 5V + V = 6V substitute these value in the equation number (1) $$ \text p \times 5V + 10p \times V = p` \times 6V $$ $$ \text 5pV + 10pV = 6p`V $$ $$\Rightarrow 15pV = 6p`V $$ $$\Rightarrow p` = \dfrac{{15p}}{{6p}} = \dfrac{5}{2}p $$ According to boyle's law p \times 5V = p \times {V_1}$Where${V_1}$is the volume in the first part after undergoing an isothermal process. After putting these value we get $p \times 5V = \dfrac{5}{2}p \times {V_1}$$ \Rightarrow 5pV = \dfrac{5}{2}p{V_1}$ $\therefore {V_1} = 2V$Similarly, applying boyle's law for second pa$10p \times V = p \times {V_2}$Where,${V_2}$is the volume in the second part after undergoing an isothermal process. Now,$10p \times V = \dfrac{5}{2}p \times {V_2}$$ \Rightarrow 10pV = \dfrac{5}{2}p{V_2}$ $\therefore {V_2} = 4V$
2V and 4V are the volume of first part and second part respectively.

so, option C is correct.

Note:
First we need to draw a diagram for better understanding the question and we have to remember the isothermal process, so PV remains constant. When the piston moves freely till the pressure becomes the same for both the parts then by applying Boyle's law we have found the volume of both the parts. We have found the volume of both the parts.