Question

A closed coil consists of $500$ turns on a rectangular frame of the area $4.0c{m^2}$ and has a resistance of $500\Omega$ . The coil is kept with its plane perpendicular to a uniform magnetic field of $0.2wb/{m^2}$ , the amount of charge flowing through the coil if it is turned over. (Rotate through ${180^0}$ ): -
(A) $1.6 \times {10^{ - 3}}C$
(B) $16 \times {10^{ - 3}}C$
(C) $0.16 \times {10^{ - 3}}C$
(D) $160 \times {10^{ - 3}}C$

Answer 1

We know that the moving charge produces a magnetic field. Similarly, when a current-carrying wire is kept in a magnetic field it experiences a force on it. Magnetic flux is the measure of the field lines passing through the area.

Complete Step By Step Answer:

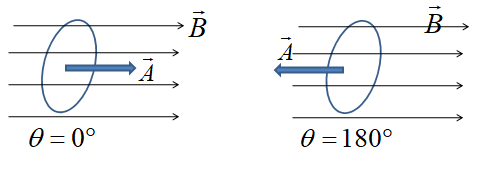
Let us first write the information given in the question.
Number of turns $n = 500$ , area $A = 4c{m^2} = 4 \times {10^{ - 4}}{m^2}$ , resistance $R = 500\Omega$ , and magnetic field $B = 0.2wb/{m^2}$
We have to calculate the amount of charge flowing through the coil.
Magnetic flux is given by the following formula.
$\phi = nBA\cos \theta$
Where $n$ is a number of turns, $B$ is a magnetic field, $A$ is the area, and $\theta$ is the angle between the area vector and the magnetic field.
So, let us calculate the change in magnetic flux when it is turned over (rotated by $180$ -degrees).
$\vartriangle \phi = nBA\cos 0 - \left( {nBA\cos 180} \right)$
Let us simplify the expression.
$\vartriangle \phi = nBA + nBA = 2nBA = 2 \times 500 \times 0.2 \times 4 \times {10^{ - 4}}$
$\vartriangle \phi = 8 \times {10^{ - 2}}$
The charge flowing through the area is given by the following formula.
$\vartriangle Q = \dfrac{{\vartriangle \phi }}{{resistance}} = \dfrac{{8 \times {{10}^{ - 2}}}}{{500}} = 1.6 \times {10^{ - 4}}C = 0.16 \times {10^{ - 3}}C$
Hence, the correct option is (C) $0.16 \times {10^{ - 3}}C$ .

Note:
The more the number of turns, the more will be the current through the coil.
Magnetic flux depends on the cosine of the angle. It means maximum flux will pass through the surface when the area vector and magnetic field will be in the same direction and no flux will pass when both are perpendicular to each other.