Question

A closed circular loop of $200\;$ turns of mean diameter $50\;cm$ & having a total resistance of $10\Omega$ is placed with its plane at a right angle to a magnetic field of strength ${10^{ - 2}}$ Tesla. Calculate the quantity of electric charge passed through it when the coil is turned through ${180^\circ }$ about an axis in its plane.

Answer 1

As the coil is rotated, the magnetic flux passing through the surface of the loop changes. This change in the magnetic flux creates an induced e.m.f. in the coil, which causes a current to flow through it. Since the current is the amount of charge flowing per unit time, the total charge passed through the coil can be also determined.
Formula used:
$\phi = NBA\cos \theta$

Complete step by step answer:
A closed circular loop, when placed with its plane at a right angle to the magnetic field, looks like this-

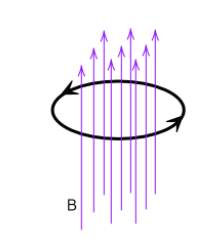
When the loop is turned by ${180^\circ }$, the direction of the magnetic flux passing through it reverses.
We know that the magnetic flux $\left( \phi \right)$ passing through a loop is given by-
$\phi = NBA\cos \theta$
where,
$N$ is the number of turns of the coil,
$B$ is the strength of the magnetic field,
$A$is the area enclosed by the loop of wire,
and $\theta$ is the angle made between the area vector and the magnetic field.
The area vector of a loop of wire is given by the right-hand thumb rule, it is normal to the plane and points in the direction the thumb of a right hand would point if the fingers are curled in the direction of current flow.
Thus, at the start, the angle made by the area of the loop and the magnetic field $\theta = {0^\circ }$
The flux passing through the coil is given by-
${\phi _1} = NBA\cos \theta$
Keeping the value of $\theta = {0^\circ }$
We have, $\cos {0^\circ } = 1$
Therefore,
${\phi _1} = NBA$
When the coil is rotated by ${180^\circ }$, the angle made by the area vector and the magnetic field becomes, $\theta = {180^\circ }$.
We know that,
$\cos {180^\circ } = - 1$
Keeping this value in the equation,
${\phi _2} = NBA\cos \theta$
We obtain-
${\phi _2} = - NBA$
The change in flux is given by-
$\Delta \phi = {\phi _2} - {\phi _1}$
Putting the values,
$\Delta \phi = - NBA - NBA$
$\Delta \phi = - 2NBA$
Let $t$ be the time taken by the flux to change.
Then the e.m.f. induced by the change in the magnetic flux is given by,
$\varepsilon = - \dfrac{{\Delta \phi }}{t}$
$\Rightarrow \varepsilon = \dfrac{{2NBA}}{t}$ $...(1)$
e.m.f. can also be written as-
$\varepsilon = IR$
where $I$ is the current and $R$ is the resistance.
Current is equal to the charge $\left( q \right)$ flowing per unit time $\left( t \right)$,
So,
$\varepsilon = \dfrac{{qR}}{t}$ $...(2)$
Combining equations $(1)$ and $(2)$ ,
$\dfrac{{qR}}{t} = \dfrac{{2NBA}}{t}$
$\Rightarrow qR = 2NBA$
It is given in the question that,
The resistance of the coil, $R = 10\Omega$
Number of turns, $N = 200$
The radius of the coil is $25\;cm$which makes the area-$A = \pi {R^2} = 1962.5c{m^2}$
In SI units,
$A = 0.1962{m^2}$
Strength of the magnetic field, $B = {10^{ - 2}}$Tesla
Therefore, the charge-
$q = \dfrac{{2 \times 200 \times {{10}^{ - 2}} \times 0.1962}}{{10}}$
$\Rightarrow q = \dfrac{{4 \times 0.1962}}{{10}}$
$\Rightarrow q = 7.848 \times {10^{ - 2}}C$

The charge passed through the coil is equal to $7.848 \times {10^{ - 2}}C$.

Note: The direction of the area vector is always normal to its plane, but the point of the arrow ( up or down) generally depends on the other quantities accompanying it. Otherwise, the arrow of the area vector can point in both directions.