Question

A clock face has negative charges -q, -2q, -3q, … , -12q fixed at the position of the corresponding numerals on the dial. The clock hands do not disturb the net field due to point charges. At what time does the hour hand point in the same direction as the electric field at the centre of the dial?

Answer 1

Begin by first determining the net direction of the electric field between diametrically opposite charges, keeping in mind that the field is stronger towards a bigger charge. We also know that the net charge across diametrically opposite charges will be the difference between them and this remains the same for all diametrically opposite charges. Then, find the resultant direction of the electric field from the net direction of electric field vectors obtained above. Do so by accounting for the resultant of two vectors of same magnitude and the angle subtended between them if the resultant also has the same magnitude. Then, find the angle at which the resultant field vector lies, and this should give you the position of the hour hand, which in turn should help you determine the time at which the electric field direction at the centre coincides with the hour hand.

Formula Used:
Magnitude of electric field E produced by a point charge q, at a distance r away from the point charge in frees space is given by:
$E = \dfrac{1}{4\pi\epsilon_0}\dfrac{q}{r^2} = \dfrac{kq}{r^2}$

Complete step-by-step answer :
Let us begin by sketching out what the clock looks like. We have negative charges -q, -2q, -3q, … , -12q arranged as the numbers on a clock dial. Each of these point charges produce an electric field corresponding to their magnitude. Owing to the linear nature of electric field lines, let us consider charges that are diametrically opposite to each other.
We need to first determine the resultant electric field at the centre of the clock as a result of all these charges on the dial of the clock.
We know that the electric field produced by a point charge is given by:
$E = \dfrac{1}{4\pi\epsilon_0}\dfrac{q}{r^2} = \dfrac{kq}{r^2}$, where $k=\dfrac{1}{4\pi\epsilon_0}$, q is the magnitude of the point charge and r is the distance from the point charge.
From this we have $E \propto q$ and $E \propto \dfrac{1}{r^2}$.
Since all the charges on the clock are the same distance from the centre, the only influencing factor will be $E \propto q$. And we also know that electric field lines are always directed towards a negative point charge. Thus, the electric field between two charges is directed towards the charge with a bigger magnitude. This results in electric field lines directed as indicated by lines $E_1, E_2, E_3, E_4, E_5$and $E_6$ in the figure.
Now, since the difference in the charges between the diametrically opposite point charges is -6q, for all such charges the magnitude of the electric field experienced is the same, say E. Therefore, the magnitude of vectors lines $E_1, E_2, E_3, E_4, E_5$ and $E_6$ will be E each.

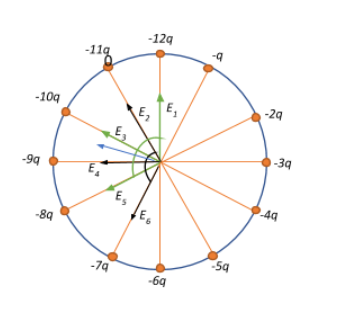
Also, every point charge is placed on the dial at an angle of $\dfrac{360}{12} = 30^{\circ}$ apart.
We know that if the magnitude of two vectors and their resultant is the same, then the angle between the two vectors will be $120^{\circ}$
Therefore, if we begin at the electric field vector $E_1$, the next influencing field vector which is at $120^{\circ}$ from it is vector $E_5$. The resultant of these two field vectors will be at $60^{\circ}$ which is nothing but in the direction of the vector $E_3$.
Therefore, the total magnitude of the electric field in the direction of vector $E_3$ will be the sum of the original field magnitude, and the resultant field of vectors $E_1$ and $E_5$ will be $|E_3|= E+E = 2E$
Similarly, if we begin at the electric field vector $E_2$, the next influencing field vector which is at $120^{\circ}$ from it is vector $E_ 6$. The resultant of these two field vectors will be at $60^{\circ}$ which is nothing but in the direction of the vector $E_4$.
Therefore, the total magnitude of the electric field in the direction of vector $E_4$ will be the sum of the original field magnitude, and the resultant field of vectors $E_2$ and $E_6$ will be $|E_4|= E+E = 2E$
Therefore, the net electric field at the centre of the dial will be the resultant of the total electric field vectors $E_3$ and $E_4$. Since the magnitude of $E_3$ and $E_4$ are the same, we can say that the resultant field vector will be at the bisector line of the angle between the two. This is indicated by the blue line in the figure.
Thus, the net electric field due to all these point charges arranged about the dial of the clock is directed between charges -9q and -10q. If the hour hand was at this position, it would indicate a time of $9:30$.
In conclusion, the time at which the electric field and the hour hand point in the same direction will be when the clock strikes $9:30$.

Note : Let us see the physical proof for why the angle between two vectors $E_1, E_2$ of the same magnitude (say, E) whose resultant $E_R$ also has the same magnitude E are aligned at an angle $120^{\circ}$.
The resultant of the two vectors using parallelogram law of vector addition is given as:
$E_R^2 = E_1^2 + E_2^2 + 2E_1 E_2 cos\theta$
$\Rightarrow E^2 = E^2+E^2+2(E)(E)cos\theta \Rightarrow E^2 = 2E^2+2E^2cos\theta \Rightarrow E^2 = 2E^2(1+cos\theta)$
$\Rightarrow \dfrac{1}{2} – 1 =cos\theta \Rightarrow \theta = cos^{-1}\left(-\dfrac{1}{2}\right) = 120^{\circ}$
This justifies our claim in the problem.