Question

A circus artist is climbing a $20$ m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is $30^\circ$ .

Answer 1

Hint : The given question is based on the topic “trigonometry”. In this question we need to find the height of the pole. To find the height we use trigonometry because the surface of the ground, the height of the pole and the line of elevation all together form a right angle triangle with 90 degrees between the pole and the ground. To solve this problem first we need to draw the diagram based on the details given in the question. Then we can start to solve it.

Complete step-by-step answer :
In this problem,
A circus artist is climbing a $20$ m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground.
The angle made by the rope with the ground level is $30^\circ$ .
Let us draw an image based on the given details,

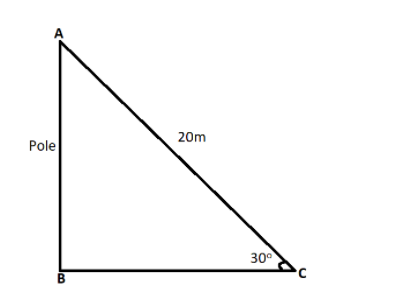
Let $AB$ be the vertical pole and $AC$ be the rope of length $20$ m, which the circus artist is climbing.
Let us assume the height of the vertical pole $AB$ be $h$ .
By given we can say that,
$AC = 20$
$\angle ACB = 30^\circ$
From the above diagram we can say that it is a right-angled triangle. Here we know a side of the triangle and its opposite angle.
Therefore,
In $\Delta ABC$ ,
$\sin 30^\circ = \dfrac{{AB}}{{AC}}$
The value of $\sin 30^\circ$ is $\dfrac{1}{2}$, by substituting this,
$\dfrac{1}{2} = \dfrac{h}{{20}}$
By cross multiplying we will get,
$2h = 20$m
Now we get the value of $2h$ . To find the value of $h$, 2 in multiplication when came across $=$ , it will become division.
$h = \dfrac{{20}}{{10}}$
$h = 10$m.
Therefore, the height of the pole is $10$ m.
So, the correct answer is “$10$ m”.

Note : Distance is usually the 'base' of the right-angled triangle formed by the height of pole and line of sight.

1. Compulsorily draw the diagram then only we will get an idea about the question.
2. When a side of the triangle and its opposite angle is known then we can use $\sin \theta$.