Question

A circular wire loop of radius R is placed in the X-Y plane centered at the origin O. A square loop of side a (a << R) having two turns is placed with its center at $z=\sqrt{3}R$ along the axis of the circular wire loop, as shown in the figure. The plane of the square loop makes an angle of ${{45}^{0}}$with respect to the z-axis. If the mutual inductance between the loops is given by $\dfrac{{{\mu }_{0}}{{a}^{2}}}{{{2}^{p/2}}R}$, then the value of p is –

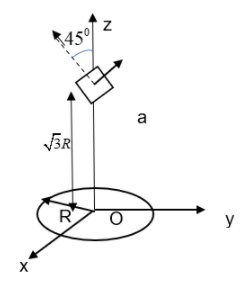
A.7
B.17
C.14
D.8

Answer 1

Mutual inductance occurs when a changing magnetic flux in one of the coils induces a magnetic flux in the other. Consider one of the loops with current flowing and causing the other to have an induced current. We can use the magnetic field due to the circular loop to find the inductance.

Complete answer:
Let us consider the circular loop as the current carrying wire. The magnetic field due to the circular loop on the square loop can be given by derivation from Biot-Savart law as –

& B=\dfrac{{{\mu }_{0}}2\pi i{{R}^{2}}}{4\pi {{({{R}^{2}}+3{{R}^{2}})}^{\dfrac{3}{2}}}} \\\ & B=\dfrac{{{\mu }_{0}}i}{16R} \\\ \end{aligned}$$  Now, let us compute the mutual induction experienced by the coils. We should remember that the square loop is in an angle with the plane, so the magnetic flux will be reduced by a factor of the cosine. The magnetic flux is given by, $$\begin{aligned} & \phi =BA\cos \theta \\\ & here, \\\ & B=\dfrac{{{\mu }_{0}}i}{16R} \\\ & A={{a}^{2}} \\\ & \Rightarrow \phi =\dfrac{{{\mu }_{0}}i}{16R}{{a}^{2}}\cos \theta \\\ \end{aligned}$$ Now, the mutual inductance is given by, $$\begin{aligned} & M=\dfrac{N\phi }{i} \\\ & \Rightarrow M=\dfrac{2}{i}\dfrac{{{\mu }_{0}}i}{16R}{{a}^{2}}\cos \theta \\\ & \therefore M=\dfrac{{{\mu }_{0}}{{a}^{2}}}{{{2}^{3+\dfrac{1}{2}}}R} \\\ & \Rightarrow M=\dfrac{{{\mu }_{0}}{{a}^{2}}}{{{2}^{\dfrac{7}{2}}}R} \\\ \end{aligned}$$ The power of 2 is $$\dfrac{7}{2}$$. The value of p is 7 **The correct answer is option A.** **Additional Information:** The mutual inductance is dependent on area of cross section, number of turns and the current flow. **Note:** Mutual inductance is the working principle of the transformers. The self-inductance which is the reactance offered by a material against the current flow is due to the development of magnetic field around it. It is reluctant to change. The induction is the resistance to change of magnetic flux.