Question

A circular tube of mass $M$ is placed vertically on a horizontal surface as shown in the figure. Two small spheres, each of mass $m$, just fit in the tube, are released from the top. If $\theta$ gives the angle between the radius vector of either ball with the vertical, obtain the value of the ratio $M/m$ if the tube breaks its contact with ground when $\theta = {60^ \circ }$. Neglect any friction.

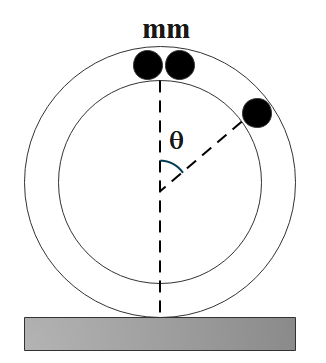
\eqalign{ & {\text{A}}{\text{. 1:2}} \cr & {\text{B}}{\text{. 1:3}} \cr & {\text{C}}{\text{. 2:1}} \cr & {\text{D}}{\text{. 2:3}} \cr}

Answer 1

Firstly, find the expression for the velocity of the small spheres using the concept of conservation of energy. Then, form a mathematical equation of all the forces acting on the system and balance them. Lastly use the expression for forces necessary to keep the circular tube in contact with the ground

Formula Used:
Velocity, $v = \sqrt {2gh}$

Complete step-by-step answer:
Given:
The mass of the circular tube, $M$
The mass of the small spheres, $m$
The angle between radius vector of the sphere with the vertical, $\theta = {60^ \circ }$
Initially, both the spheres are at the top of the circular tube, let this height be h. At this particular instant, the energy of the system is completely potential energy. And when the spheres strike at the bottom of the circular tube, then the energy of the system is purely kinetic. Let the velocity of the ball be v.

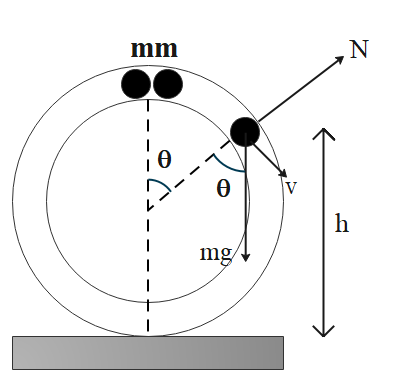
By law of conservation of energy, we know that the initial energy of the system is equal to the final energy of the system. So we have:
Potential energy = Kinetic energy
\eqalign{ & mgh = \dfrac{1}{2}m{v^2} \cr & \Rightarrow 2gh = {v^2} \cr & \therefore v = \sqrt {2gh} \cr}
But from figure we know that $h = R\left( {1 - \cos \theta } \right)$
Substituting the value of h in the expression for velocity, we get:
$v = \sqrt {2gR\left( {1 - \cos \theta } \right)} \cdots \cdots \cdots \cdots \left( 1 \right)$
Now, balancing the forces that will act on the system, we have:
$N + mg\cos \theta = \dfrac{{m{v^2}}}{R}$
Substituting the value of velocity from equation (1), we get:
\eqalign{ & N + mg\cos \theta = \dfrac{{m\left[ {2gR\left( {1 - \cos \theta } \right)} \right]}}{R} \cr & \Rightarrow N + mg\cos \theta = 2mg\left( {1 - \cos \theta } \right) \cr & \Rightarrow N + mg\cos \theta = 2mg - 2mg\cos \theta \cr & \Rightarrow N = 2mg - 3mg\cos \theta \cdots \cdots \cdots \cdots \left( 2 \right) \cr}
Now, because the circular tube breaks its contact with ground, that means:
$2N\cos \theta = + Mg$
Substituting value of N in from equation (2), we have:
\eqalign{ & 2\left( {2mg - 3mg\cos \theta } \right)\cos \theta = + Mg \cr & \Rightarrow 4mg\cos \theta - 6mg{\cos ^2}\theta = Mg \cr & \Rightarrow 4mg\left( {\dfrac{1}{2}} \right) - 6mg\left( {\dfrac{1}{4}} \right) = Mg{\text{ }}\left[ {\because \theta = {{60}^ \circ }\left( {{\text{given}}} \right)} \right] \cr & \Rightarrow 2m - \dfrac{3}{2}m = M \cr & \Rightarrow \dfrac{{4m - 3m}}{2} = M \cr & \Rightarrow \dfrac{m}{2} = M \cr & \therefore \dfrac{M}{m} = \dfrac{1}{2} \cr}
Therefore, the correct answer is A. i.e., the ratio $M/m$ if the tube breaks its contact with ground is ${\text{1:2}}$.

Note: The normal force N is introduced in mechanics, and is a component of the contact force. The normal force always acts perpendicular to the surface of the object that is in contact. It is a resultant of the forces between the constituents of the actual constraints, and the constituents of the object.