Question

A circular ring of radius $R$ and mass $m$ made of a uniform wire of cross-sectional area $A$ is rotated about a stationary vertical axis passing through the centre and perpendicular to the plane of the ring. The breaking stress of the material of the ring is ${\sigma _{\text{b}}}$ . If Young’s modulus of the material is $Y$ , then determine the maximum angular speed ${\omega _{\max }}$ at which the ring may be rotated without failure.

Answer 1

First of all, we will resolve the acting forces which will give us the net tension force on the ring. Again, we will find the centripetal force which is the result of the angular motion directed towards the centre of the ring. We will equate the net tension force with the centripetal force followed by rearrangement of the expression and manipulating accordingly to obtain the result.

Complete step by step answer:
In the given question, we are supplied with the following data:
The circular ring has a radius of $R$ and mass $m$ made of a uniform wire of cross-sectional area $A$ .
The ring rotates about its axis which is perpendicular to the plane of the ring and the axis passes through the centre of the ring.
The breaking stress of the material of the ring is ${\sigma _{\text{b}}}$ .
We are asked to find the maximum angular speed at which the ring may be rotated without failure.
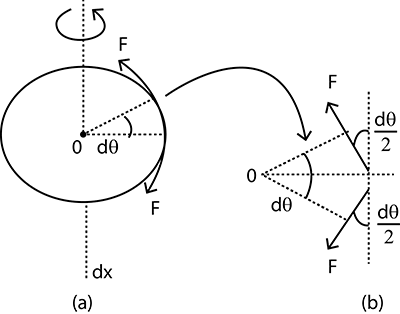
To begin with, we will assume the small section subtends an angle of $d\theta$ .
As the ring is rotational motion, so it experiences a tension force $F$ , which is about the ring’s circumference as described by the diagram below:

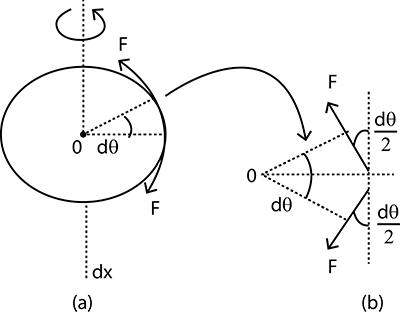
The resultant or net tangential component of this tension force will be zero, since the tensions will act in opposite directions and cancel out each other.
So, the tension force present on the ring is totally from the horizontal components of the tension force, which is mathematically shown by:
${T_{{\text{net}}}} = F\sin \left( {\dfrac{{d\theta }}{2}} \right) + F\sin \left( {\dfrac{{d\theta }}{2}} \right)$
$\Rightarrow {T_{{\text{net}}}} = 2F\sin \left( {\dfrac{{d\theta }}{2}} \right)$
Since, $d\theta$ is a very small angle.
So,
$\sin \left( {\dfrac{{d\theta }}{2}} \right)\, = \dfrac{{d\theta }}{2}$
Now, we use this value in the above expression:
${T_{{\text{net}}}} = 2F\sin \left( {\dfrac{{d\theta }}{2}} \right)$
$\Rightarrow {T_{{\text{net}}}} = 2F \times \dfrac{{d\theta }}{2}$
$\Rightarrow {T_{{\text{net}}}} = Fd\theta$
Again, we consider the mass of the small component to be $dm$ . So, the length of the arc which is subtended by this small angle will be $\dfrac{{d\theta }}{{2\pi }}$ . This is because the length of the boundary of the ring is $2\pi$ .
The small mass of the ring composed in this small component will now be:
$dm = m \times \dfrac{{d\theta }}{{2\pi }}$
Now, we write the expression for the centripetal force which is experienced by this small component, is given by:
${F_{\text{c}}} = \left( {dm} \right) \times \omega _{\max }^2 \times R$
$\Rightarrow {F_{\text{c}}} = \left( {m \times \dfrac{{d\theta }}{{2\pi }}} \right) \times \omega _{\max }^2 \times R$
Again, we can write from the term stress:
${\sigma _{\text{b}}} = \dfrac{F}{A}$
$\Rightarrow F = A \times {\sigma _{\text{b}}}$
As we have,
${T_{{\text{net}}}} = Fd\theta$
So, we can do some modifications in the equation as:
${T_{{\text{net}}}} = A \times {\sigma _{\text{b}}}d\theta$
We know, centripetal force is the horizontal force, so we can equate the two expressions as:
${F_{\text{c}}} = {T_{{\text{net}}}}$
$\Rightarrow \left( {m \times \dfrac{{d\theta }}{{2\pi }}} \right) \times \omega _{\max }^2 \times R = A \times {\sigma _{\text{b}}}d\theta$
$\Rightarrow \dfrac{{m \times \omega _{\max }^2 \times R}}{{2\pi }} = A \times {\sigma _{\text{b}}}$ $\Rightarrow \omega _{\max }^2 = \dfrac{{2\pi A{\sigma _{\text{b}}}}}{{mR}}$
Again, we simplify,
$\Rightarrow {\omega _{\max }} = \sqrt {\dfrac{{2\pi A{\sigma _{\text{b}}}}}{{mR}}}$
Hence, the maximum angular speed ${\omega _{\max }}$ at which the ring may be rotated without failure is $\sqrt {\dfrac{{2\pi A{\sigma _{\text{b}}}}}{{mR}}}$ .

Note: It is important that we must resolve all the forces which are important as it helps us for the clear understanding leading to the various effects on the system, otherwise it will produce irrelevant results which will confront the original result. A material can experience a limiting stress before it breaks off and this varies with different materials.