Question

A circular racecourse track has a radius of $500\;m$ and is banked to $10^{\circ}$. If the coefficient of friction between tyres of a vehicle and the road surface is $0.25$, compute:
A). The maximum speed to avoid slipping
B). The optimum speed to avoid wear and tear

Answer 1

Try to illustrate the situation which may help you account for all the components of forces contributing to the equilibrium of the vehicle. In other words, resolve the normal reaction, frictional force, and weight into their respective components and deduce which of the components act in the vertical and horizontal directions. Play around with the equations thus obtained to arrive at an expression for velocity. Do not forget to account for the banking of the road, the frictional force, as well as the centrifugal force acting on the vehicle as it moves in a circular path.

Formula Used:
Maximum speed to avoid slipping: $v_{max} = \sqrt {\dfrac{rg(tan \theta + \mu)}{ 1 – \mu tan\theta }}$
Optimum speed to avoid wear and tear: $v_{optimum} = \sqrt{rg\;tan\theta}$
Here, r is the track radius, g is the acceleration due to gravity, $\theta$ is the banking angle, and $\mu$ is the coefficient of friction.

Complete step-by-step solution:
__

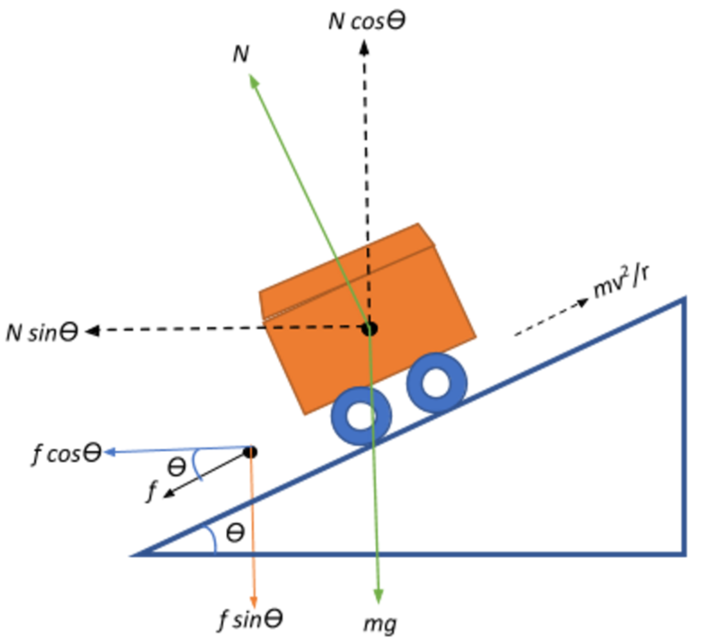
Let us deconstruct the question to derive an expression for a vehicle moving on this banked racetrack in general
Let that mass of the vehicle be $m$, and let it move with a velocity $v$. Since its moving in a circular racetrack with radius $r$, it experiences a centrifugal force of magnitude $F_{c} = \dfrac{mv^2}{r}$ directed outwards.
Let $\theta$ be the angle of banking and let $f$ be the frictional force acting between the road and the tyres.
Note that we divide the forces in play into their respective components to ease our understanding and simplify calculations. These are shown in the diagram.
Now, for a balanced system, the
total upward force = total downward force
$\Rightarrow N\;cos\theta = mg + f\;sin\theta \Rightarrow mg = N\;cos\theta – f\;sin\theta$
Similarly, we look at the lateral forces, which for a balanced system:
$\dfrac{mv^2}{r} = N\;sin\theta + f\;cos\theta$.
On dividing the above two equations we get:
$\dfrac{\dfrac{mv^2}{r}}{mg} = \dfrac{ N\;sin\theta + f\;cos\theta }{N\;cos\theta – f\;sin\theta} \Rightarrow \dfrac{v^2}{rg} = \dfrac{ N\;sin\theta + f\;cos\theta }{N\;cos\theta – f\;sin\theta}$
Now, substituting frictional force $f = \mu N$ in the above equation we get:
$\dfrac{v^2}{rg} = \dfrac{ N\;sin\theta + \mu N\;cos\theta }{N\;cos\theta – \mu N\;sin\theta} \Rightarrow \dfrac{v^2}{rg} = \dfrac{ sin\theta + \mu cos\theta }{cos\theta – \mu sin\theta}$
Now, dividing both the numerator and the denominator by $cos\theta$:
$\dfrac{v^2}{rg} = \dfrac{ tan \theta + \mu }{1 – \mu tan\theta} \Rightarrow v = \sqrt {\dfrac{rg(tan \theta + \mu)}{ 1 – \mu tan\theta }}$
a). We can now calculate the maximum speed to avoid slipping:
This is basically the maximum speed that the vehicle can travel under the influence of friction. This is given by the expression we derived above:
($tan 10^{\circ} = 0.1763$)
$v_{max} = \sqrt {\dfrac{rg(tan \theta + \mu)}{ 1 – \mu tan\theta }} = \sqrt {\dfrac{500 \times 9.8 (0.1763 + 0.23)}{ 1 – (0.25 \times 0.1763)}} = \sqrt{2185.182}$
$\Rightarrow v_{max} = 46.75\;ms^{-1}$
b). The optimum speed to avoid wear and tear can be given by disregarding friction and taking $\mu = 0$, in which case:
$v_{optimum} = \sqrt{rg\;tan\theta} = \sqrt{500 \times 9.8 \times 0.1763} = \sqrt{863.87}$
$\Rightarrow v_{optimum} = {29.39 \;ms^{-1}}$

Note: It is always essential to deduce which component of the forces are acting in which direction. By resolving our influencing forces to their respective components, we are able to isolate only those components of forces that contribute to the equilibrium of the body in that direction.
Also, remember that for the first part we considered an expression for velocity when friction was prevalent. This is because to avoid slipping the vehicle must get a grip, and this grip is provided by the friction between the road and the tyres.
For the second part, we discount friction only because the major source of wear and tear of the tyres is due to frictional forces that act between the tyres and the road.