Question

A circular platform is mounted on a frictionless vertical axle. If the radius R=2m and its moment of inertia about the axle is $200kg{m^2}$. It is initially at rest. A 50 kg man stands on the edge of the platform and begins to walk along the edge at the speed of $1m{s^{ - 1}}$ relative to the ground. Time taken by the man to complete one revolution is-
A. $\dfrac{{3\pi }}{2}s$
B. $2\pi s$
C. $\dfrac{\pi }{2}s$
D. $\pi s$

Answer 1

Hint: In the given question the system was initially at rest and no external torque acts on it. Thus the total angular momentum must be conserved. Additionally, using the relation between angular velocity and linear velocity we can find these terms. Finally, Speed is the ratio of distance traveled and time. So time will be the distance traveled over speed.

Formula Used:
\eqalign{ & \dfrac{{dL}}{{dt}} = {\tau _{ext}} \cr & {\text{where }}{\tau _{ext}}{\text{ is the external Torque on the system,}} \cr & L{\text{ is the angular momentum of the system}}{\text{.}} \cr}
\eqalign{ & {\text{ }}v = R\omega \cr & v{\text{ is the linear velocity,}} \cr & {\text{R is the radius of the platform,}} \cr & \omega {\text{ is the angular velocity of the platform}}{\text{.}} \cr}
\eqalign{ & {\text{Speed = }}\dfrac{{{\text{Distance}}}}{{{\text{Time}}}} \cr & \Rightarrow {\text{Time}} = \dfrac{{{\text{Distance}}}}{{{\text{Speed}}}} \cr}

Complete step by step answer:
Consider the given system of a circular platform mounted on a frictionless vertical axle, and a man of 50 kg walking along the edge of this platform with speed of $1m{s^{ - 1}}$, as shown below in the diagram:

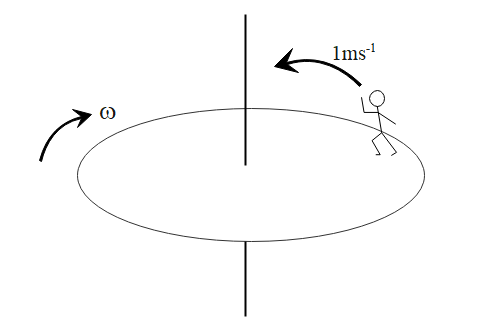
Given:
The radius of the circular platform, R= 2m
Moment of Inertia of Circular platform, I=$200kg{m^2}$
Mass of the man, m=50 kg,
Speed of the man, $v = 1m{s^{ - 1}}$

Initially the entire system was at rest. And no external Torque is acting on the system.
i.e. ${\tau _{ext}} = 0$
But we know that:
\eqalign{ & \dfrac{{dL}}{{dt}} = {\tau _{ext}} \cr & {\text{where }}{\tau _{ext}}{\text{ is the external Torque on the system,}} \cr & L{\text{ is the angular momentum of the system}}{\text{.}} \cr}
So, if the total external torque on a system is zero, its angular momentum remains constant. In other words the angular momentum of the system is conserved.
Applying Law of conservation of angular momentum we get:
$m\left( v \right)\left( R \right) = I\omega$
Substituting the given values we get:
\eqalign{ & 50 \times 1 \times 2 = 200\omega \cr & \Rightarrow \omega = \dfrac{{100}}{{200}} \cr & \therefore \omega = 0.5{\text{ radians}} \cr}
Now the resultant angular velocity of the entire system will be the vector sum of the angular velocity of the man and the platform.
\eqalign{ & {\omega _R} = \dfrac{v}{R} - \omega {\text{ }}\left[ {{\text{Using }}v = R\omega } \right] \cr & \Rightarrow {\omega _R} = \dfrac{1}{2} - 0.5{\text{ radians}} \cr & \Rightarrow {\omega _R} = 0.5{\text{ radians}} \cr}
Now, the distance travelled is the circumference of the circular path i.e., ${\text{2}}\pi {\text{R}}$
But we know that:
\eqalign{ & {\text{Speed = }}\dfrac{{{\text{Distance}}}}{{{\text{Time}}}} \cr & \Rightarrow {\text{Time}} = \dfrac{{{\text{Distance}}}}{{{\text{Speed}}}} \cr}
Substituting values in the formula, we get:
\eqalign{ & {\text{Time,}}T = \dfrac{{2\pi R}}{{\omega R}} \cr & \Rightarrow T = \dfrac{{2\pi }}{\omega } \cr & \therefore T = 2\pi \sec \cr}
Therefore, the correct option is B. i.e., $2\pi s$.

Note: Angular momentum is a physical quantity that comes into action for a rotating body only. Mathematically, it is the product of the magnitude of the linear momentum of the body and the perpendicular distance from the axis of rotation.