Question
Question: A circular platform is free to rotate in a horizontal plane about a vertical axis passing through it...
A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given as angular velocity ω0 when a tortoise moves along a chord of the platform with a constant velocity (with respect to platform), the angular velocity of the platform ω(t) will vary with time t as:
A. 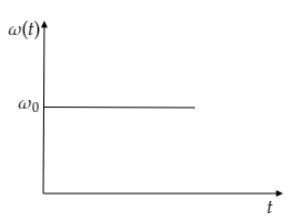
B. 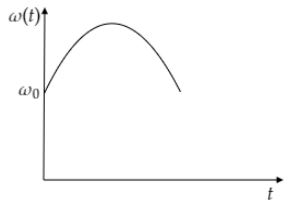
C. 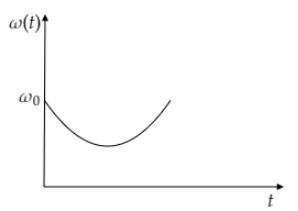
D. 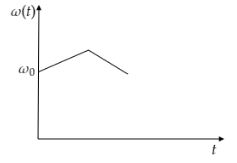
Solution
As long as there is no external torque on the system the total angular momentum of the system is constant. i.e., total initial angular momentum of the system is equal to the total final angular momentum of the system. The angular momentum of the system will vary inversely with the square of distance between the tortoise and the center of the platform. i.e., the angular momentum of the system will increase first as the distance between the tortoise and the center of the platform decreases and then the angular momentum will decrease as the distance between the tortoise and the center of the platform increases.
Complete step by step answer:
It is given that a circular platform rotates in a horizontal plane about its axis passing through its center. A tortoise is placed at the edge of the platform. The initial angular velocity of the platform-tortoise system is ω0. Now the tortoise moves along a chord of the platform with a constant velocity w.r.t. the platform. Let M and m be the masses of the platform and the tortoise respectively. R is the radius of the platform. Let’s draw the diagram which depicts the question.
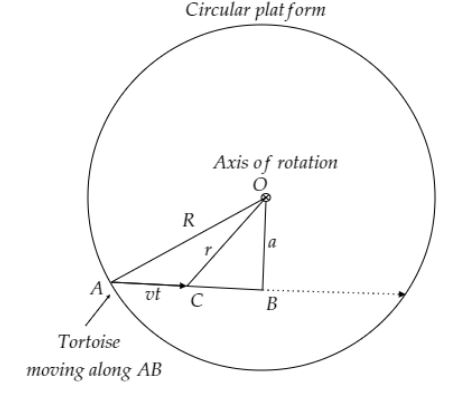
From the above diagram, the moment of inertia of the system at the point A is,
IA=Iplatform+IA,tortoise
Iplatform is the moment of inertia of the platform about the axis passing through the center of the platform.
Iplatform=2MR2
IA,tortoise is the moment of inertia of the tortoise at the point A about the axis passing through the center of the platform.
IA,tortoise=mR2
Therefore, IA=2MR2+mR2
The total moment of inertia at the point C is,
IB=Iplatform+IB,tortoise
Where IB,tortoise is the moment of inertia of the tortoise at the point C about the axis passing through the center of the platform.
From the above diagram, we found
IB,tortoise=mr2
Consider the right-angle triangle ABO, AB=R
Let OB=a
Therefore, AB=R2−a2
Now consider the right angle-triangle CBO,
CO=r
⇒CB=AB−AC
Since the tortoise moves with uniform velocity v, The displacement AC=vt. Where t is the time taken by the tortoise to reach the point C.
So, CB=R2−a2−vt
Now, (CO)2=(OB)2+(CB)2
Substitute all the required values in the above formula. We got,
r2=a2+(R2−a2−vt)2
Substitute the value of r in IB,tortoise=mr2
IB,tortoise=m[a2+(R2−a2−vt)2]
Now calculate IB. We got,
IB=2MR2+m[a2+(R2−a2−vt)2]
Since there is no external torque acting on the system, The total angular momentum of the system is conserved i.e., total angular momentum at point A = total angular momentum at point B.
⇒IAωA=IBωB
It is given that the initial angular velocity ωA=ω0.
And ωB=ω(t)
⇒ω(t)=IBIAω0
Substitute the value of IA and IB in the above formula.
⇒ω(t)=2MR2+m[a2+(R2−a2−vt)2](2MR2+mR2)ω0 …… (1)
At t=0, ω(t)=ω0
It is now clear that ω(t) varies nonlinear curve with time t as from above equation we have ω(t)∝t21.
To know the nature of nonlinear, replace a2+(R2−a2−vt)2=r2 in the equation (1). We got,
⇒ω(t)=2MR2+mr2(2MR2+mR2)ω0
∴ω(t)∝r21
Since, the tortoise moves along the chord, the distance between the tortoise and the center of the platform r decreases first till a and then increases again. Hence, ω(t) first increases upto r=a and then decreases. The variation of ω(t) with t is as follows.
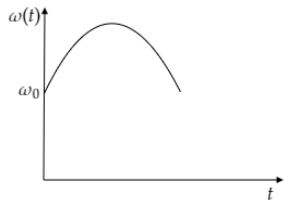
Hence, the correct option is B.
Note: The platform is a solid circular disk. Hence, its moment of inertia about the axis passing through its center is I=2MR2. Where, M and R are the mass and radius of the disk respectively. The moment of inertia of a particle of mass m about an axis is I=mr2. Where, r is the distance of the particle from the axis of rotation.
