Solveeit Logo
Login

Question

Question: A circular plate of area \[0.4\,c{m^2}\] is kept at a distance of 2 m isotropic (uniform in all dire...

A circular plate of area 0.4 cm20.4\,c{m^2} is kept at a distance of 2 m isotropic (uniform in all direction) source of power πW\pi W. Find the amount of energy received on plates in 5 secs.

Explanation

Solution

Use the relation between power and energy to determine the energy emitted by the source. The energy received by the surface depends on the surface area. To solve this question, consider the source is placed at the centre of the sphere of radius 2 m emitting the energy in all directions and find out the energy received by the sphere in 5 seconds.

Formula used:
P=WtP = \dfrac{W}{t}
Here, W is the energy and t is the time.

Complete step by step answer:
We know the relation between power and energy. The power is the energy received or lost per unit time.
P=WtP = \dfrac{W}{t}
Here, W is the energy and t is the time.
Therefore, the energy received becomes,
W=PtW = Pt
Consider an imaginary sphere around the source such that the source is at the centre of the sphere and the circular plate is placed somewhere on this sphere as shown in the figure below.

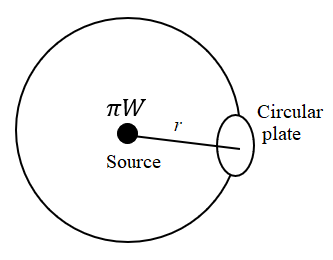
In the above figure, r is the radius of the imaginary sphere. It has a value of 2 m.
The energy emitted by the source in 5 seconds is,
W=(πW)(5 sec⁡)W = \left( {\pi W} \right)\left( {5\,\sec } \right)
⇒W=5π J\Rightarrow W = 5\pi \,J
The energy received by the surface area of the sphere of radius 2 m is,
4πr2=5π J4\pi {r^2} = 5\pi \,J
The energy received by the circular plates of area 0.4 cm20.4\,c{m^2} is W′W'. Therefore,
0.4 cm2=W′0.4\,c{m^2} = W'
Therefore, we can write,
4πr20.4×10−4 m2=5π JW′\dfrac{{4\pi {r^2}}}{{0.4 \times {{10}^{ - 4}}\,{m^2}}} = \dfrac{{5\pi \,J}}{{W'}}
Substitute 2 m for r in the above equation.
4π(2 m)20.4×10−4 m2=5π JW′\dfrac{{4\pi {{\left( {2\,m} \right)}^2}}}{{0.4 \times {{10}^{ - 4}}\,{m^2}}} = \dfrac{{5\pi \,J}}{{W'}}
⇒W′=(0.4×10−4 m2)(5π J)16π m2\Rightarrow W' = \dfrac{{\left( {0.4 \times {{10}^{ - 4}}\,{m^2}} \right)\left( {5\pi \,J} \right)}}{{16\pi \,{m^2}}}
⇒W′=1.25×10−5 J\Rightarrow W' = 1.25 \times {10^{ - 5}}\,J
Therefore, the energy received by the plate in 5 sec is 1.25×10−5 J1.25 \times {10^{ - 5}}\,J.

Note:
To use the formula for power, convert the unit of area of the surface into S.I. units. Here, in 5π W5\pi \,W, W is the unit of power (Watt) and not the energy.The power is the energy received or lost per unit time.