Question

A circular loop of string rotates about its axis on a frictionless horizontal plane at a uniform rate so that the tangential speed of any particle of the string is v. If a small transverse disturbance is produced at. a point of the loop, with what speed (relative to the string) will this disturbance travel on the string?

Answer 1

in order to solve the question, we will use the formula of centrifugal force on the small part of ring by using that we will find the force of that part then we will integrate it for whole loop after then we will equate the whole force with the twice tension after then we will use the formula of velocity of transverse vibration to find the speed (relative to the string) that create disturbance in travelling of string

Formula used:
$F = (mRd\theta ){\omega ^2}R$
Here, $F$ refers to centrifugal force, $M$ refers to mass per unit length of the string, $R$ refers to radius of the loop, $ω$ refers to angular velocity and $V$ refers to linear velocity of the string.
$V = \sqrt {\dfrac{T}{m}}$
Here, $V$ refers to Velocity of transverse vibration, $M$ refers to mass and $T$ refers to tension.

Complete step by step answer:

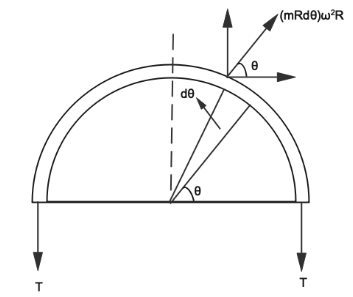
In the question we are given that a circular loop of string rotates about its axis on a frictionless horizontal plane at a uniform rate so that the tangential speed of any particle of the string is $v$. If a small transverse disturbance is produced at a point of the loop. In order to solve the question easily we will take the half loop. This half loop experiences centrifugal force at every point, away from the center this centrifugal force is balanced by the tension 2T.

Now we will consider an element of angular part $d\theta$ at angle $\theta$ for solving the question we will consider a small element symmetric to this centrifugal force
$F = (mRd\theta ){\omega ^2}R$
$\Rightarrow \;Length{\text{ }}of{\text{ }}element{\text{ }} = {\text{ }}Rd\theta$
$\Rightarrow mass{\text{ }} = {\text{ }}mRd\theta$
Resolving into rectangular components net force on the two symmetric elements. Horizontal components $(mRd\theta ){\omega ^2}R\cos \theta$ will cancel each other. Now solving the vertical component. Vertical component 2 twice the force because force of both the quarter of ring adds up,
$dF = 2m{R^2}d\theta {\omega ^2}\sin \theta$

Now we will integrate the force from $0{\text{ to }}\dfrac{\pi }{2}$
$\int {dF} = \int\limits_{0\pi }^{\dfrac{\pi }{2}} {2m{R^2}d\theta {\omega ^2}\sin \theta }$
Total force we will get by integrating
$F = 2m{R^2}{\omega ^2}\left[ { - \cos \theta } \right]$
$\Rightarrow 2m{R^2}{\omega ^2}$
As we can see in the diagram force is equal to twice tension
$2T = 2m{R^2}{\omega ^2}$
$\Rightarrow T = m{R^2}{\omega ^2}$
Velocity of transverse vibration
$V = \sqrt {\dfrac{T}{m}}$
Now we will insert the value of $T$ in the above equation
$V = \sqrt {\dfrac{{m{R^2}{\omega ^2}}}{m}}$
$M$ will be cut off and the square root we get $V$ as
$\therefore V = R\omega$

Hence, speed $V = R\omega$ creates the disturbance in travelling on the string (relative to the string).

Note: There might be a chance to make the mistake by trying to solve the problem by taking the full loop but by taking the full loop we increase the complexity of the problem but to keep the question we will take half loop and then we will use integration to solve the answer by integration we will use small part of loop and we get answer of whole loop.