Question

A circular loop of radius R carrying current I lies in the x-y plane with its centre at origin. The total magnetic flux through the x-y plane is ?

Answer 1

In magnetism, we know magnetic field lines form closed loops which originate from the North pole and enter in the South pole. and Magnetic flux is the amount of magnetic field lines entering in a given surface area. We will figure out the nature of magnetic field lines produced in a circular loop and then will calculate magnetic flux.

Complete answer:
According to the question, Let a circular loop is placed on the X-Y plane carrying current I having radius $R$ and centre at origin. Let us assume current is flowing in clockwise direction as seen from above so, From right hand thumb rule, The direction of magnetic field lines will be in negative $Z$ direction which is into the XY plane.

Hence direction of Magnetic field is $- \hat k$ but since, magnetic field lines always form a closed loop means as soon as they will originate from the circular loop in downward direction , they will end up again entering in the loop by changing their direction to make a complete loop as shown in the diagram.

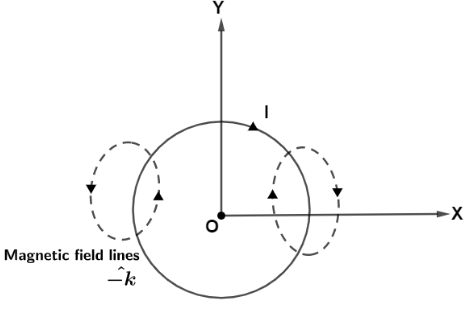
Hence, from the diagram we can see that, Number of magnetic field lines entering into the circular loop is equal to the number of magnetic field lines leaving the loop. Which means the net number of magnetic field lines inside the surface area of the loop is zero which results in magnetic flux as zero.

Hence, net magnetic flux through the circular loop will be zero.

Note: It should be remembered that, no matter in which plane the loop is placed the net flux will be always zero and generally The magnetic flux is the dot product between magnetic field vector and surface area vector and it is written as ${\phi _B} = \vec B.\vec A$ where B,A are the magnetic field and Surface area vectors.