Question

A circular hole of radius 1m is cut off from a disc of radius 6cm. The centre of the hole is 3cm from the centre O of the disc. The centre of mass of the remaining disc is

Answer 1

Here we can use the concept of negative mass by assuming that an equal amount of negative mass of the removed part is added to the whole of the disc. And then we can use the equation for finding the centre of mass of two bodies to find the centre of mass. This value will be the value for the centre of mass of the remaining disc.

Complete step by step answer:
The disc has a radius,
$R = 6\,m$
It is given that a circular hole is cut off from this disc.
The radius of the circular hole,
$r = 1\,m$
The centre of the hole is at a distance $3\,m$ from the centre of mass O of the disc.
We need to calculate the centre of mass of the remaining disc.
Assume that the thickness is $t$.
Then the volume is area multiplied by thickness.
$V = At$
Area of base is,
$A = \pi {R^2}$
$\Rightarrow V = \pi {R^2}t$
Let the density be $\rho$. then we have
$\rho = \dfrac{M}{V}$
$\Rightarrow M = \rho V = \rho \pi {R^2}t$
On substituting the value of radius, we get
$\Rightarrow M = 36\pi \rho t$ …………………………….(1)
Similarly, the mass of the removed part, $m$ can be written as
$\Rightarrow m = \rho \pi {r^2}t$
On substituting the value of the radius of cut out the part, we get
$\Rightarrow m = \rho \pi t$ …………………..(2)
On dividing equation (1) and (2) we get
$\Rightarrow m = \dfrac{M}{{36}}$
Now let us use the negative mass concept. That is, we can consider that the disc is whole and a part of $- \dfrac{M}{{36}}$ mass is placed at a distance $3\,m$ away from its centre. So, we get the same total mass as we would get if there is a hole of the same portion.
The centre of mass of the inner disc will be at its centre. That is $3\,m$ away from the centre of the larger disc.
Let us take the coordinate of the centre of mass of the larger disc as $\left( {0,0} \right)$. That is the origin.

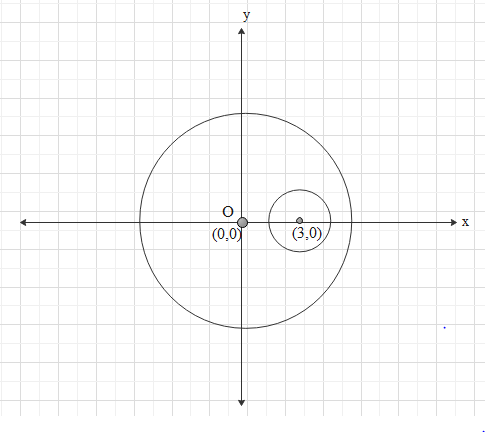
The centre of mass of inner disc will be at $\left( {3,0} \right)$
Now we can calculate the centre of mass of the system as a whole.
The centre of mass of two body is given as
${X_{cm}} = \dfrac{{{m_1}{x_1} + {m_2}{x_2}}}{{{m_1} + {m_2}}}$
${Y_{cm}} = \dfrac{{{m_1}{y_1} + {m_2}{y_2}}}{{{m_1} + {m_2}}}$
Now let us substitute the values,
$\Rightarrow {X_{cm}} = \dfrac{{M \times 0 - \dfrac{M}{{36}} \times 3}}{{M - \dfrac{M}{{36}}}}$
Since the $x$ coordinate of the larger disc is zero and the $x$ coordinate of the smaller disc is 3.
$\Rightarrow {X_{cm}} = \dfrac{{\dfrac{{ - 3}}{{36}}}}{{\dfrac{{35}}{{36}}}} = \dfrac{{ - 3}}{{35}}\,$
If we substitute the values in
$\Rightarrow {Y_{cm}} = \dfrac{{{m_1}{y_1} + {m_2}{y_2}}}{{{m_1} + {m_2}}}$
We get,
$\Rightarrow {Y_{cm}} = \dfrac{{M \times 0 - \dfrac{M}{{36}} \times 0}}{{M - \dfrac{M}{{36}}}} = 0$
Since the y coordinate of the centre of mass of the outer and inner disc is zero.
So, we get the centre of mass at $\left( { - \dfrac{3}{{35}},0} \right)$

That is the new centre of mass will be at a distance $\dfrac{3}{{35}}$ to the left of the centre O of the given disc.

Note:
Remember that the concept of negative mass is physically not possible. Mass cannot be negative but in order to solve the problem, we assumed the mass to be negative. So, when we needed to subtract a mass from the given mass, we changed the situation to adding an equal amount of negative mass so that the final effect is the same.