Question

A circular disc of radius R is removed from a bigger circular of radius$2R$, such that the circumference of the discs coincide. The centre of mass of the new disc is $\alpha R$ distance from the centre of the bigger disc. The value of $\alpha$is:
A. $1/3$
B. $1/2$
C. $1/6$
D. $1/4$

Answer 1

Concept of centre of mass is used as after removing the disc from bigger circle, there will be change in centre of mass of the new disc obtained .Also as the disc is uniform, so even after cutting the disc from bigger disc, there will be no change in density that is density remains constant.

Formula used:
${x_{cm}} = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + ..... + {m_n}{x_n}}}{{{m_1} + {m_2} + .... + {m_n}}}$

Complete step by step answer:
Let us consider the circular disc to be lying in the x-y plane as shown in the figure such that the centre of the bigger circle of radius $2R$ lies at origin $O$and then the centre of the second disc of radius $R$at $x = R$ and let us consider the complete mass of the disc be$M$.

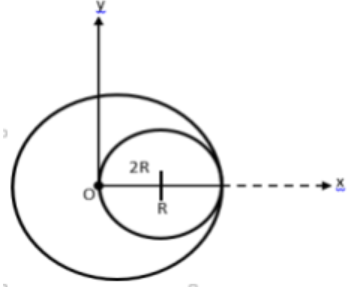
Centre of mass of a body is a point where the entire mass of a system may be supposed to be concentrated.
Then, the position vector of centre of mass of smaller disc is $\overrightarrow {{x_1}} = R\hat i$
Let the centre mass of the new disc be $(x,y)$
Then, the position vector of this will be $\overrightarrow {{x_2}} = x\hat i + y\hat j$
Now, as the disc is uniform, so density will be constant
Density, $\rho = \dfrac{{mass}}{{Area}}$
For disc,
As density constant
So, $\dfrac{{Mass}}{{Area}} = cons\tan t$
So, $\dfrac{{mass\,\,of\,\,smaller\,\,disc}}{{mass\,\,of\,\,l\arg er\,\,disc}} = \dfrac{{area\,\,of\,\,smaller\,\,disc}}{{Area\,of\,\,l\arg er\,\,disc}}$
$\Rightarrow \dfrac{{{M_1}}}{M} = \dfrac{{{A_1}}}{A} = \dfrac{{\pi {R_2}}}{{\pi {{(2R)}^2}}} = \dfrac{{\pi {R^2}}}{{4\pi {R^2}}} = \dfrac{1}{4}$
So, mass of the new disc will be ${M_2} =$mass of larger disc $=$mass of smaller disc
$= M - {M_1} = \dfrac{3}{4}M$
Now, for complete disc, centre of mass will
$\overrightarrow {{x_{cm}}} = \dfrac{{{M_1}\overrightarrow {{x_1}} + {M_2}\overrightarrow {{x_2}} }}{{{M_1}{M_2}}}$
$O = \dfrac{{\dfrac{M}{4} \times R\hat i + \dfrac{{3M}}{4}(x\hat i + y\hat j)}}{M}$
$O\hat i + O\hat j = \dfrac{{\left( {\dfrac{M}{4}R + \dfrac{{3M}}{4}x} \right)\hat i + \dfrac{{3M}}{4}y\hat j}}{M}$
Equating the coefficient of $\hat i\,and\,\,\hat j$ $\dfrac{{\dfrac{M}{4}R + \dfrac{{3M}}{4}x = 0}}{M}$
$\Rightarrow \dfrac{R}{4} + \dfrac{{3x}}{4} = 0 \\\ \Rightarrow \dfrac{{3x}}{4} = \dfrac{{ - R}}{4} \\\$
$\Rightarrow x = \dfrac{{ - R}}{3}$
Similarly, $\dfrac{{3M}}{4}y = 0$
$\Rightarrow \dfrac{{3y}}{4} = 0$
$\Rightarrow y = 0$ So, the distance of centre of mass of new disc $= x = \dfrac{R}{3}$
But according to question $x = \alpha R$
On equating, we get
$\alpha = \dfrac{1}{3}$

So, the correct answer is “Option B”.

Note:
As all options are positive, so negative signs can be neglected. This can also be solved using the moment of inertia of discs.
Also while equating coefficients, the coefficient of i on L.H.S. will be equated with coefficient of i on R.H.S.