Question

A circular disc of radius $\frac{R}{2}$ is cut from a circular disc of radius R and mass 4M as shown in figure. Then moment of inertia about the centre of the disc and $\perp$er to its plane is

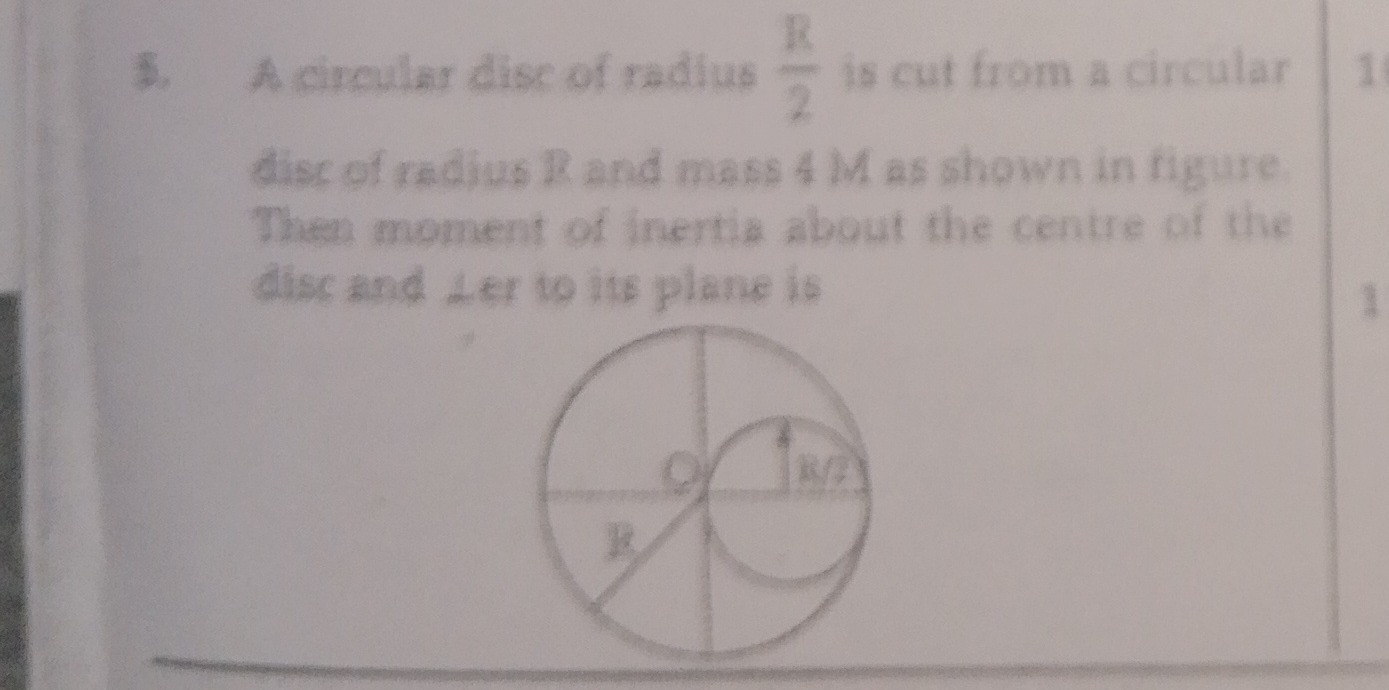
Answer 1

The moment of inertia is $\frac{13MR^2}{8}$.

Answer 2

Solution

1. Original Disc:

   • Mass = 4M, Radius = R
   • Moment of inertia about its center: $$I_\text{large}=\tfrac{1}{2}(4M)R^2=2MR^2.$$

2. Cut-out Disc:

   • Radius = $\tfrac{R}{2}$.
   • Area density: $\sigma=\dfrac{4M}{\pi R^2}$.
   • Mass of cut-out: $$m=\sigma\cdot \pi\left(\tfrac{R}{2}\right)^2=\dfrac{4M}{\pi R^2}\cdot \pi\frac{R^2}{4}=M.$$
   • Its moment inertia about its own center: $$I_\text{cm}=\tfrac{1}{2}m\left(\tfrac{R}{2}\right)^2=\frac{MR^2}{8}.$$
   • The center of the cut-out is at a distance $d=\tfrac{R}{2}$ from the center of the large disc.
   • Using the parallel axis theorem, its moment inertia about the large disc’s center: $$I_\text{cut}=I_\text{cm}+m\,d^2=\frac{MR^2}{8}+M\left(\frac{R}{2}\right)^2=\frac{MR^2}{8}+\frac{MR^2}{4}=\frac{3MR^2}{8}.$$

3. Net Moment of Inertia:

   Subtract the cut-out contribution from the original disc:

   $$I_\text{net}=I_\text{large}-I_\text{cut}=2MR^2-\frac{3MR^2}{8}=\frac{16MR^2-3MR^2}{8}=\frac{13MR^2}{8}.$$

Explanation (Minimal Core):

• Total inertia of full disc: $2MR^2$.
• Cut-out (mass M) inertia about its own center: $\tfrac{MR^2}{8}$; add offset inertia $M\left(\tfrac{R}{2}\right)^2=\tfrac{MR^2}{4}$ giving $\tfrac{3MR^2}{8}$.
• Subtract to yield $2MR^2-\tfrac{3MR^2}{8}=\frac{13MR^2}{8}$.