Question
Question: A circular conducting loop of radius R carries current I. Another straight infinite conductor carryi...
A circular conducting loop of radius R carries current I. Another straight infinite conductor carrying current I passes through the diameter of this loop as shown in the figure. The magnitude of force exerted by the straight conductor of the loop is,
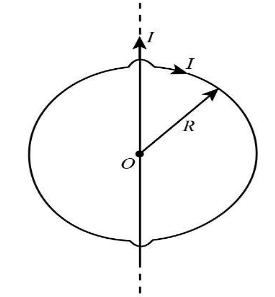
(A) πμ0I2
(B) μ0I2
(C) 2πμ0I2
(D) πμ0I2
Solution
We will use the expression for the magnetic field due to the straight conductor at a point on the loop that is in direct proportionality with the current flowing through it and inversely with the distance between them.
Complete step by step answer:
Let us consider point P and point Q, as shown in the figure below. We will also consider an element of radius R at point P having an angle dθ.
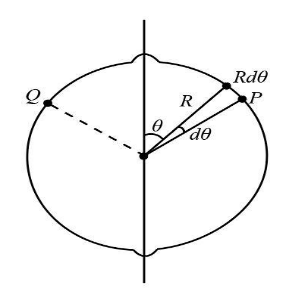
We can write the magnitude of the force exerted by the straight conductor at point P as below:
B=2πμ0rI……(1)
Here B is the magnetic field at point P, μ0 is the magnetic permeability of free space and r is the perpendicular distance between the straight conductor and point P.
We can resolve the radius R into two components, one in horizontal and other in the vertical direction. We can write the expression for the horizontal component as below which is equal to the distance between the straight conductor and point P.
r=Rsinθ
We will substitute Rsinθ for r in equation (1) to get the expression for force due to the straight conductor at point P.
B=2πμ0RsinθI
We can write the expression for the magnetic force at point P due to the straight conductor as below:
dF=I⋅dl⋅B……(2)
Here dl is the length of length at which force is acting.
We can write the expression for elemental length dl as below:
dl=Rdθ
We can substitute Rdθ for dl in equation (2).
Using the concept of thumb rule, we can say that the force at point P and point Q is acting tangentially to the loop. We can resolve the elemental force dF in x-direction and y-direction, the x component of both the forces is cancelling each other and y component is the final value of resultant force; therefore we can write:
F′=2dFsinθ
We will substitute RBldθ for dF in the above expression.
F′=2(RBldθ)sinθ
We will now substitute 2πμ0RsinθI for B in the above expression and integrating it to find the magnitude of the force on the loop.
Here F is the resultant force on the loop.
Therefore, the magnitude of force due to the straight conductor on the loop is μ0I2, and option (B) is correct.
Note: We can note that we integrated the final expression of force from zero to π because we just considered the half of the loop, which is starting from zero and going up to π. We could have done it differently by considering the elemental forces at different places.
