Question

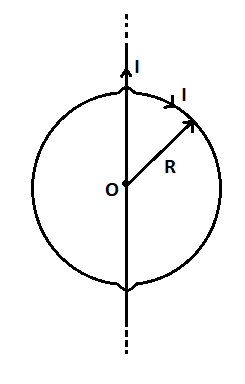
A circular conducting loop of radius $R$ carries a current $I$. Another straight infinite conductor carrying I passes through the diameter of this loop as shown in the figure. The magnitude of force exerted by the straight conductor on the loop is

A. $\pi {\mu _0}{l^2}$
B. ${\mu _0}{l^2}$
C. $\dfrac{{{\mu _0}{l^2}}}{{2\pi }}$
D. $\dfrac{{{\mu _0}{l^2}}}{\pi }$

Answer 1

The question talks about a conductor which is circular in shape and a straight cylindrical conductor which has no end or limit that are placed in a magnetic field for magnetic flux or field lines to act on.

Complete step by step answer:
We are given that a circular conducting loop of radius $R$ carries a current $I$ and another straight infinite conductor carrying I passes through the diameter of this loop as shown in the above figure.
We have to calculate the magnitude of force exerted by the straight conductor on the loop.
There exists a relationship between force and other parameters like magnetic flux density, where length and current are included in the formula.
From the distance round a circle or circumference of circle, which is that of the circular loop = $F = \dfrac{{{\mu _o}{l^2}}}{{2\pi }} \times 2\pi$ and also the area of the straight infinite conductor is same as the area of a cylinder = $2\pi rl$
Using
$F = BIL \to \left( 1 \right)$, where F is the force, B is the magnetic field line density or magnetic flux density, I is the current and L is the length
If $B = \dfrac{{{\mu _0}{l_1}}}{{2\pi d}} \to \left( 2 \right)$
Then we will substitute equation 2 into equation 1
$F = \dfrac{{{\mu _0}{l^2}d}}{{2\pi d}}$
Where length can as well be replaced by distance that exist between the loop
$F = \dfrac{{{\mu _o}{l^2}}}{{2\pi }} \times 2\pi = {\mu _o}{l^2}$
So therefore the right option is Option B.

Note: Other parameters to look out for is flux density, power applied or produced in the course of applying the magnetic flux, torque, flux density and also these conductors might be inclined or tilted at certain angles either to the horizontal direction or vertical direction.