Solveeit Logo
Login

Question

Question: A circular coil with a cross-sectional area of \(4c{{m}^{2}}\) has 10 turns. It is placed at the cen...

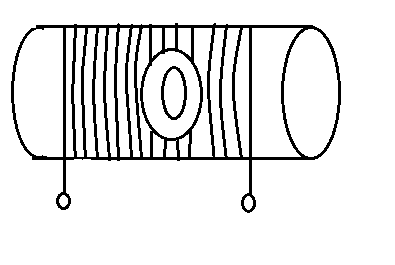
A circular coil with a cross-sectional area of 4cm24c{{m}^{2}} has 10 turns. It is placed at the centre of a long solenoid that has 15 turns/cm and a cross-sectional area of 10cm210c{{m}^{2}} , as shown in the figure. The axis of the coil coincides with the axis of the solenoid. What is their mutual inductance?

Explanation

Solution

Hint: When two coil circuits near each other and current in one of the coils are changing when EMF is induced in the neighbouring coin placed in a manner is called mutual induction. S.I. a unit of mutual induction is Henry denoted by H which is equal to volt second per ampere.

Complete step by step solution:
First, let’s understand what the question wants to understand.
We have a long solenoid on which a coil is wounded with 10 turns only and the coil cross-section area is 4cm24c{{m}^{2}}. This coil is placed at the centre of the solenoid. A number of turns of a solenoid are 15 per centimetre and the cross-sectional area is 10cm210c{{m}^{2}}.
Aim: What is mutual inductance between coil and solenoid.
Let, number of turns of coil N1=10{{N}_{1}}=10, area cross of a section of coil is A1=4cm2=4×10−4m2{{A}_{1}}=4c{{m}^{2}}=4\times {{10}^{-4}}{{m}^{2}}
And the number of turns of a solenoid in=15turns/cm=1500turns/min=15turns/cm=1500turns/m, area of cross-section is 10cm2=10×10−4m2;A2=10−310c{{m}^{2}}=10\times {{10}^{-4}}{{m}^{2}};{{A}_{2}}={{10}^{-3}}
We know that mutual induction is given by,
Mutual Induction(M)=μ0nN1A1cos⁡α\text{Mutual Induction(M)}={{\mu }_{0}}n{{N}_{1}}{{A}_{1}}\cos \alpha
Where,  ∝=angle between B⃗andA1~\propto =\text{angle between }\vec{B} and {{A}_{1}}
Therefore, Mutual Induction(M)=4π×10−7×1500×10×4×10−4×cos⁡0\text{Mutual Induction(M)}=4\pi \times {{10}^{-7}}\times 1500\times 10\times 4\times {{10}^{-4}}\times \cos 0
M=7.54×10−6HM=7.54\times {{10}^{-6}}H
M=7.54μHM=7.54\mu H
Mutual inductance is given by M=7.54μHM=7.54\mu H.

Answer is option (A).

Note: Coefficient of mutual induction or mutual inductance of two coils is defined as the ratio of e.m.f. Induced in one coil to the rate of change of current in the other coil. Mutual induction (L) depends upon the shape and size of the coil, number of turns, separation between the coil and angular orientation between the coil and medium between two coins. Note that along with mutual induction, self-induction also takes place.