Solveeit Logo
Login

Question

Question: A circular coil of radius \(10cm\), 500 turns and resistance \(2\Omega \) is placed with its plane p...

A circular coil of radius 10cm10cm, 500 turns and resistance 2Ω2\Omega is placed with its plane perpendicular to the horizontal component of the earth's magnetic field. It is rotated about its vertical diameter through 180∘{180^ \circ }m in 0.25 s. What is the current induced in the coil?
(Horizontal component of the earth’s magnetic field at that place is 3.0×10−5T3.0 \times {10^{ - 5}}T)
A. 1.9×10−3A1.9 \times {10^{ - 3}}A
B. 2.9×10−3A2.9 \times {10^{ - 3}}A
C. 3.9×10−3A3.9 \times {10^{ - 3}}A
D. 4.9×10−3A4.9 \times {10^{ - 3}}A

Explanation

Solution

Hint: Change in Magnetic flux linked with the coil leads to induced voltage or emf. It is given by Faraday’s law of induced emf ε=−Ndϕdt\varepsilon = - N\dfrac{{d\phi }}{{dt}} where N is number of turns of coil, ϕ\phi is magnetic flux and ε\varepsilon is induced emf.

Formula Used:
1. Faraday’s law of induced emf, ε=−Ndϕdt\varepsilon = - N\dfrac{{d\phi }}{{dt}} …… (a)
2. Magnetic flux, ϕ=B.A=BAcos⁡θ\phi = B.A = BA\cos \theta …… (b)
3. Ohm’s Law, I=εRI = \dfrac{\varepsilon }{R} …… (c)

Complete step by step answer:
Given,
Number of turns, N=500N = 500
Magnetic field perpendicular to cross section area, BH=3×10−5T{B_H} = 3 \times {10^{ - 5}}T
Resistance present in the coil, R=2ΩR = 2\Omega
Total time taken to rotate between initial and final position, Δt=0.25s\Delta t = 0.25s
Total angle rotated, Δθ=180∘\Delta \theta = {180^ \circ }

Diagram:
Given below schematic diagram depicting the situation:

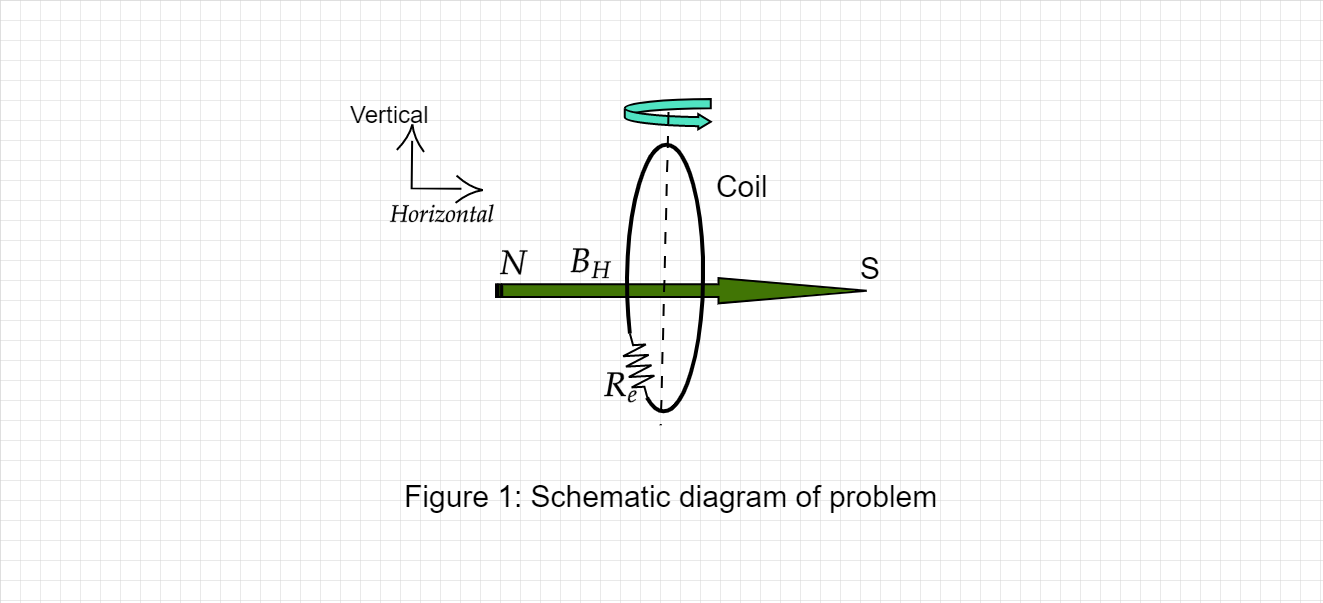
Step 1 of 6:

Initially, plane of the coil is perpendicular to BH{B_H}
Substituting values in equation (b) gives Initial magnetic flux ϕi=BH.Acos⁡0{\phi _i} = {B_H}.A\cos 0 as angle between normal of plane and field is 0
⇒ϕi=BHA\Rightarrow {\phi _i} = {B_H}A …… (1)

Step 2 of 6:

Finally, plane of the coil is again perpendicular to BH{B_H} but antiparallel
Substituting values in equation (b) gives Final magnetic flux ϕf=BH.Acos⁡(180){\phi _f} = {B_H}.A\cos (180)
⇒ϕf=−BHA\Rightarrow {\phi _f} = - {B_H}A …… (2)

Step 3 of 6:

Change in magnetic flux =Δϕ=ϕf−ϕi\Delta \phi = {\phi _f} - {\phi _i}
⇒Δϕ=−BHA−BHA=−2BHA\Rightarrow \Delta \phi = - {B_H}A - {B_H}A = - 2{B_H}A …… (3)

Step 4 of 6:
Induced emf in the coil due to change in magnetic flux given by equation (a), ε=−Ndϕdt=−NΔϕΔt\varepsilon = - N\dfrac{{d\phi }}{{dt}} = - N\dfrac{{\Delta \phi }}{{\Delta t}} for finite time and finite angle rotation approximation.

Substituting values from equation (3) in equation (a) we get
ε=−NΔϕΔt=−500−2BHAΔt\varepsilon = - N\dfrac{{\Delta \phi }}{{\Delta t}} = - 500\dfrac{{ - 2{B_H}A}}{{\Delta t}} …… (4)

Step 5 of 6:

Putting values of variables in equation (4) from the given values we get

ε=500×2×3π×10−70.25=0.00038V\varepsilon = 500 \times \dfrac{{2 \times 3\pi \times {{10}^{ - 7}}}}{{0.25}} = 0.00038V …… (5)
Step 6 of 6:

Substituting value from equation (5) in equation (C) with value of resistance we get
I=εR=0.000382AI = \dfrac{\varepsilon }{R} = \dfrac{{0.00038}}{2}A
⇒I=1.9×10−3A\Rightarrow I = 1.9 \times {10^{ - 3}}A

Correct Answer:
A. 1.9×10−3A1.9 \times {10^{ - 3}}A

Note: Here we used discrete time approximation of Faraday’s law because we have been given discrete values of time and flux change. Otherwise, we need to differentiate time varying magnetic flux linkage with the coil.