Question
Question: A circular coil of radius 10 cm and 25 turns is rotated about its vertical diameter with an angular ...
A circular coil of radius 10 cm and 25 turns is rotated about its vertical diameter with an angular speed of 40srad, in a uniform horizontal magnetic field of magnitude 5×10−2T. Calculate the maximum emf induced in the coil. Also, find the current in the coil if the resistance of the coil is 15Ω .
Solution
The concept of electromagnetic induction has to be applied. Use the faraday's law to get the variation of the induced emf due to the rotation of the Coil. Consider the peak value of the induced emf. To find the current in the coil use ohm's law in the coil.
Complete answer:
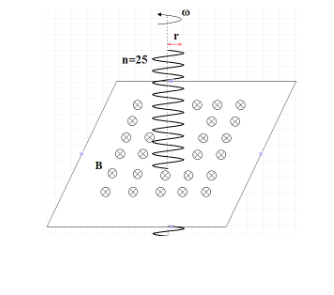
Given radius of coil r = 10cm
Number of turns in a circular coil N = 25
The angular speed of the coil omega = 40srad
The magnitude of a uniform horizontal magnetic field B=5×10−2
Area of the coil A=πr2=3.14×(10×10−2)2=0.0314m2
The resistance of the coil R=15Ω
Now, to find the induced emf, we need magnetic flux.
Magnetic flux is given by the equation,
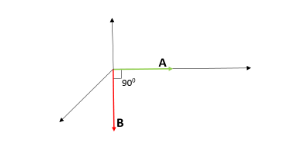
ϕ=B⋅A=BAcos(θ)
But, from the figure, we can understand that the angle between the area vector and the magnetic field is 90∘ .
Therefore, ϕ=B⋅A=BA .
Now we need to calculate the induced emf in the coil. It is given by,
Einduced=dt−dϕ=−NBdtdA=−NBAω
Where dtdA refers to the rate at which the area vector rotates which is nothing but the ω given.
So we can get the induced emf as,
Einduced=−NBAω=25(5×10−2)×(3.14×(10×10−2)2)×40=1.57V
Thus we got the induced emf using the faraday law of induction as Einduced=1.57V .
Consequently, the value of the current in the circuit can be calculated as using the ohms law as,
I=RV=151.57=0.1047A
So we finally found the value of the current as I=0.1047A using ohm’s law.
Additional Information:
Here the coil is rotating in the magnetic field which is constant. We can consider that the area vector of the coil is rotating the given angular speed and hence the derivative of the Area vector is cos term with amplitude NABω which we used in the problem.
Note:
We can solve the above in a different assuming that the loop is stationary and the field is rotating then in that case we need to evaluate the value of dtdB which is time-consuming and hence we have used the concept of the variable area vector to get the max value of the induced emf and then found the current.
