Question

A circular beam of light of diameter $d=2cm$ falls on a plane surface of glass. The angle of incidence is ${{60}^{0}}$ and the refractive index is $\mu =\dfrac{3}{2}$. The diameter of the refracted beam is –

& \text{A) 4}\text{.00cm} \\\ & \text{B) 3}\text{.00cm} \\\ & \text{C) 3}\text{.26cm} \\\ & \text{D) 2}\text{.52cm} \\\ \end{aligned}$$

Answer 1

The circular beam of light of certain diameter after moving from one medium to another refracts and as a result undergoes a change in diameter of the refracted beam. We can use the trigonometric relations to find this change in diameter.

Complete answer:
Consider a surface AB which acts as an interface between two media of which the refractive index of the second is $\mu =\dfrac{3}{2}$ as shown in the given figure. Initially the beam has a diameter ‘d’ which then passes through AB, gets refracted and finally the diameter becomes ${{d}^{'}}$.

        ![](https://www.vedantu.com/question-sets/5ea7ad7e-f258-457d-868c-6b19d8e1be646308957879393668367.png)   

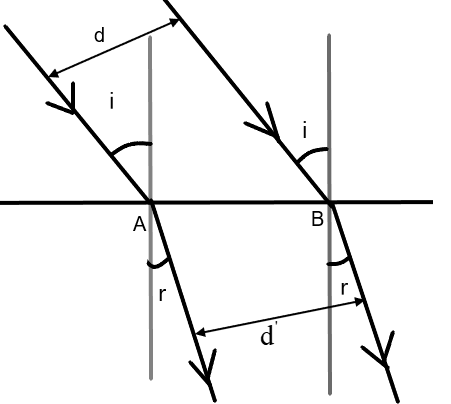
It is natural to wonder how this change in diameter happens!! The answer is simple. It is because one wavefront of the circular beam hits the interface AB at different times. Drawing a perpendicular from the one ray to the other as shown below can help us understand that.
Due to this delay of one end of the wavefront to change medium, the two ends of the wavefront start to move in different velocities, which eventually results in different diameters once both the ends of the wavefront are in the same medium.

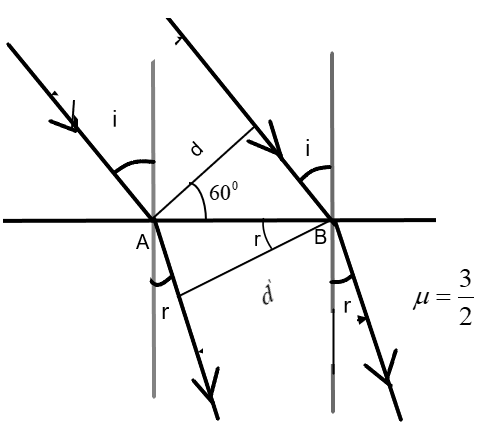
Let us consider the triangle in the first medium –

& \cos {{60}^{0}}=\dfrac{d}{AB} \\\ & \Rightarrow \text{ }d=AB\cos {{60}^{0}} \\\ & \Rightarrow \text{ }d=AB.\dfrac{1}{2} \\\ & \text{but it is already given that,} \\\ & d=2cm \\\ & \Rightarrow \text{ }AB=2d=4cm\text{ --(1)} \\\ \end{aligned}$$ Now, consider the refracted medium – $$\begin{aligned} & \cos r=\dfrac{{{d}^{'}}}{AB} \\\ & \Rightarrow \text{ }{{d}^{'}}=AB\cos r \\\ & \because \text{ }AB=4cm\text{ from (1)} \\\ & \Rightarrow \text{ }{{d}^{'}}=4\cos r \\\ \end{aligned}$$ Now, let us consider the Snell’s law for the given refraction – $$\begin{aligned} & \text{i}\text{.e}\text{.,} \\\ & \dfrac{\sin i}{\sin r}=\dfrac{{{\mu }_{2}}}{{{\mu }_{1}}} \\\ \end{aligned}$$ We can substitute the given information to get the solution. $$\begin{aligned} & \text{here, } \\\ & i={{60}^{0}},{{\mu }_{2}}=\dfrac{3}{2}\text{ and }{{\mu }_{1}}=1 \\\ & \Rightarrow \text{ }\dfrac{\sin {{60}^{0}}}{\sin r}=\dfrac{3}{2} \\\ & \Rightarrow \text{ }\sin r=\dfrac{\sqrt{3}}{2}\times \dfrac{2}{3} \\\ & \Rightarrow \text{ }\sin r=\dfrac{1}{\sqrt{3}} \\\ & \text{We can find cos r from this as - } \\\ & \cos r=\sqrt{1-{{\sin }^{2}}r} \\\ & \Rightarrow \text{ }\cos r=\sqrt{1-{{(\dfrac{1}{\sqrt{3}})}^{2}}} \\\ & \Rightarrow \,\text{ }\cos r=\sqrt{\dfrac{2}{3}} \\\ \end{aligned}$$ Now, we know the equation to find the diameter of the refracted beam in terms of cosine of the refracted angle as – $$\begin{aligned} & {{d}^{'}}=AB\cos r \\\ & \Rightarrow \text{ }{{d}^{'}}=4\times \sqrt{\dfrac{2}{3}}=3.26cm \\\ \end{aligned}$$ So, we get the diameter of the refracted circular beam to be 3.26cm. **So, the correct answer is “Option C”.** **Note:** We should know that this change in diameter is due to an angle of incidence with the normal. If we are dealing with a refraction in which the angle of incidence is zero, then there will not be any refraction and hence, no change in diameter of any beam.