Question

A circuit is connected as shown in the figure with the switch S open. When the switch is closed, the total amount of charge that flows from Y to X is

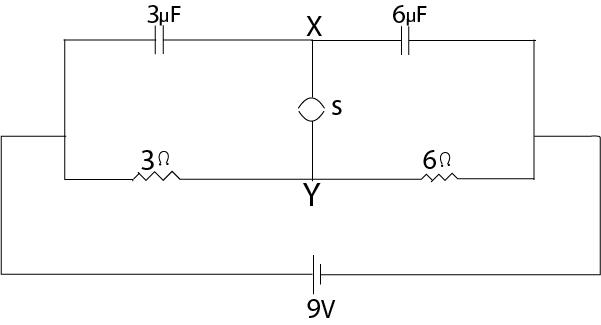
(A) 0
(B) 54μC
(C) 27μC
(D) 81μC

Answer 1

Hint
When steady state reached, the capacitors are fully charged and no current pass through the capacitor branch then we can find out the current through the resistors by using $I = \dfrac{V}{{{R_T}}}$. after that find the potentials across both the capacitor which is same as that of the potential across there resistors by using $V = IR$. Then we can find the charge on both the capacitors by using the formula $Q = CV$, then we can find the charge from Y to X by subtracting the charge of $3\mu F$ capacitor to $6\mu F$ capacitor.

Complete step by step answer
When switch S is open then at once when steady state is reached, the capacitors are fully charged and then no current will pass through the capacitor branch, then current will only pass from through the resistor branch.
Thus, current passes through the resistors are $I = \dfrac{V}{{{R_T}}}$ …………………… (1)
Where, ${R_T}$ is the total resistance
Here, it is given that ${R_1} = 3\Omega$ and ${R_2} = 6\Omega$, as R1 and R2 are the resistance and they are in series. Then the total resistance is ${R_T} = {R_1} + {R_2}$, on substituting the values, we get ${R_T} = 6 + 3 = 9\Omega$
As from the figure the applied potential is $V = 9V$
On substituting the values in equation (1), we get
$\Rightarrow I = \dfrac{9}{9} = 1A$ ……………………. (2)
Now, when switch S is closed then potential across $3\mu F$ capacitor = potential across $3\Omega$ resistance
Potential across $3\Omega$ resistance = $I \times 3 = 1 \times 3 = 3V$
Potential across $3\mu F$. capacitor = 3V
And similarly, potential across $6\mu F$ capacitor = potential across $6\Omega$ resistance = $I \times 6 = 1 \times 6 = 6V$
Now, charge on the $3\mu F$ capacitor is ${Q_1} = C{V_1} = 3 \times 3 = 9\mu C$
Similarly, charge on $6\mu F$ capacitor is ${Q_2} = 6 \times 6 = 36\mu C$
Now, we have to find out the total amount of charge flows from X to Y is
Here, -Q1 charge is shifted from the positive plate of $6\mu F$ capacitor. The remaining charge on the positive plate of the $6\mu F$ capacitor is shifted through the switch.
Thus, charge passing through the switch is = $36 - 9 = 27\mu C$
Hence, option (C) is correct.

Note
It must be noticed that when the current will pass then the capacitor will get fully charged first at that time only current passes through the resistors. After that when the capacitor will get fully charged then it starts discharging and then the current will pass through the switch till the capacitor gets fully discharged. After that the process will repeat again and again.