Question
Question: A circuit is connected as shown in the figure with the switch S open. When the switch is closed, the...
A circuit is connected as shown in the figure with the switch S open. When the switch is closed, the amount of charge that flows from Y to X is:
A) 0
B) 54μC
C) 27μC
D) 81μC
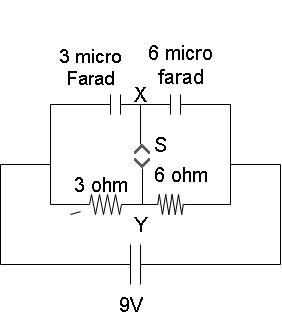
Solution
A capacitor is a device that stores energy in the electric field. It is made up of two metallic plates and separated by an insulating material known as a dielectric. The capacitors have the ability to store an electric charge in them. When the capacitor becomes fully charged, a potential difference is developed across the plates of the capacitor.
Complete step by step answer:
Step I:
When a voltage is applied across the plates of the capacitor, then the electric current starts flowing through the capacitor. The positive charge collects on one plate of the capacitor and the negative charge on another plate.
Step II:
The amount of the charge flowing through the capacitor is directly proportional to the voltage applied. The greater the voltage applied, the greater will be the charge flowing through the capacitor. The ability to store charge in the form of electric energy is known as capacitance. Its formula is
C=Vq --------------(i)
Where C is the capacitance
Q is the charge
V is the potential difference or voltage.
Step III:
When S is open, the capacitors are in series so charges each capacitor will be the same.
here, V1+V2=9 or
From equation (i) it can be written that V=Cq
⇒C1q+C2q=9
⇒q=C1+C2C1×C2×9
⇒q=3+63×6×9=18μC
When S is closed , the current through resistors I=3+69=99=1A
Potential across capacitor 3μF = potential across 3Ω resistor =3I=3V
Charge on capacitor 3μF is q=3×3=9μC
Potential across capacitor 6μF = potential across 6Ω resistor =6I=6V
Charge on capacitor 6μF=6×6=36μC
Charge flow from Y to X
⇒Δq1+Δq2=(36−18)+(18−9)=18+9=27μC
Therefore, the amount of charge flowing from Y to X is 27μC. Hence Option (C) is the right answer.
Note:
It is to be noted that apart from the voltage applied, the capacitance of a capacitor also depends on the distance of separation between the two plates. The smaller the distance, the more amount of charge will be stored on the plates. This will result in high capacitance and the energy stored will be high.
