Question

A circuit contains two inductors of self-inductance ${L_1}$ and ${L_2}$ in series as shown in the figure. If M is the mutual inductance, then the effective inductance of the circuit shown will be

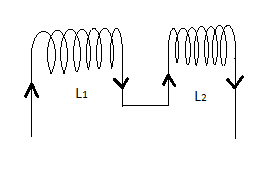
A. ${L_1} + {L_2}$
B. ${L_1} + {L_2} - M$
C. ${L_1} + {L_2} + 3M$
D. ${L_1} + {L_2} + 2M$

Answer 1

In this question, we need to determine the effective inductance of the circuit such that the two inductances are connected in a series connection, as shown in the figure. For this, we will use the properties of the inductances when connected in series while aiding the mutual inductances.

Complete step by step answer:
The self-inductance of inductor 1 $= L{}_1$
The self-inductance of inductor 2 $= L{}_2$
Mutual inductance between inductor 1 and inductor 2 is given as M.
The product of the inductance and the rate of change in the current results in the emf induced in an inductor. Mathematically, $e = L\dfrac{{di}}{{dt}}$.
The emf induced in an inductor is the summation of the emf induced in the inductor due to the inductor itself and the emf induced in the inductor due to the mutual inductance. Mathematically, $e = L\dfrac{{di}}{{dt}} + M\dfrac{{di}}{{dt}}$ where, ‘L’ is the inductance, ‘M’ is the mutual inductance and $\dfrac{{di}}{{dt}}$ is the rate of change of current.
Now let us suppose a current ‘I’ is flowing through the inductor $L{}_1$ and $L{}_2$; hence the emf induced in inductor 1 due to current I flowing through it will be
${e_1} = {L_1}\dfrac{{di}}{{dt}} + M\dfrac{{di}}{{dt}} - - (i)$
Also, the emf induced in inductor 2 due to current I flowing through it will be
${e_2} = {L_2}\dfrac{{di}}{{dt}} + M\dfrac{{di}}{{dt}} - - (ii)$
So the effective induced emf of the circuit will be given as

$${e_{effective}} = {e_1} + {e_2} \\\ = {L_1}\dfrac{{di}}{{dt}} + M\dfrac{{di}}{{dt}} + {L_2}\dfrac{{di}}{{dt}} + M\dfrac{{di}}{{dt}} \\\ = \left( {{L_1} + {L_2} + 2M} \right)\dfrac{{di}}{{dt}} \\\$$

Hence, the effective inductance of the circuit such that the two inductances are connected in a series connection is $\left( {{L_1} + {L_2} + 2M} \right)$.

So, the correct answer is “Option D”.

Note:
It is interesting to note that the induced emf in an inductor is the sum of the emf induced in an inductor due to its own inductance and the shared inductance (mutual inductance). Moreover, if the inductors are connected in parallel then, the induced emf will be the summation of the induced emf for the shared current segment also.