Question

A circuit containing a 80 mH inductor and a $60 \mu F$ capacitor in series is connected to a 230 V, 50 Hz supply. The resistance of the circuit is negligible.
a) Obtain the current amplitude and rms values.
b) Obtain the rms values of potential drop across each element
c) What is the average power transferred to the inductor?
d) What is the average power transferred to the capacitor?
e) What is the total average power absorbed by the circuit? [Average implies average value over one cycle]

Answer 1

To solve this given question, first find the angular frequency and the peak voltage using their respective formulae. We can use the formula for maximum current, substitute the values in the formula and obtain the maximum current. Take the modulus of this value and obtain the amplitude of the current.

Complete answer:

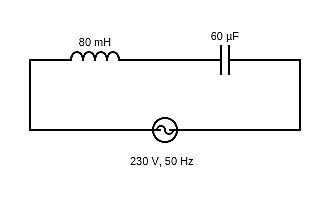
Given: Inductance, $L= 80 mH= 80 \times {10}^{-3} H$
Capacitance, $C= 60 \mu F= 60 \times {10}^{-6} F$
Supply voltage, V= 230 V
Frequency, $\nu= 50 Hz$
Angular frequency is given by,
$\omega=2\pi \nu$
Substituting values in above equation we get,
$\omega= 2 \pi \times 50$
$\Rightarrow \omega= 314 rad/s$
Peak voltage is given by,
${V}_{0}= V \sqrt{2}$
Substituting values in above equation we get,
${V}_{0}= 230 \sqrt {2}$
$\Rightarrow {V}_{0}= 325.27 V$
a) Maximum current is given by,
${I}_{0}= \dfrac { { V }_{ 0 } }{ \left( \omega L-\dfrac { 1 }{ \omega C } \right) }$
Substituting values in above equation we get,
${I}_{0}= \dfrac { 325.27 }{ \left( 314\times 80\times { 10 }^{ -3 }-\dfrac { 1 }{ 314\times 60\times { 10 }^{ -6 } } \right) }$
$\Rightarrow {I}_{0}=\dfrac { 325.27 }{ \left( 2512\times { 10 }^{ -2 }-\dfrac { 1 }{ 1884\times { 10 }^{ -5 } } \right) }$
$\Rightarrow {I}_{0}=\dfrac { 325.27 }{ \left( 25.12-53.08 \right) }$
$\Rightarrow {I}_{0}= \dfrac { 325.27 }{ -27.96 }$
$\Rightarrow {I}_{0}= -11.63A$
So, the amplitude of current is $\lvert {I}_{0} \rvert= 11.63 A$,
Now, RMS value of current will be given by,
$I=\dfrac { { I }_{ 0 } }{ \sqrt {2} }$
Substituting values in above equation we get,
$I=\dfrac {11.63}{\sqrt {2} }$
$\Rightarrow I= 8.22 A$
b) Potential difference across the inductor is given by,
${V}_{L}= I \times \omega L$
Substituting values in above equation we get,
${V}_{L}= 8.22 \times 314 \times 80 \times {10}^{-3}$
$\Rightarrow {V}_{L}= 206,484 \times {10}^{-3}$
$\Rightarrow {V}_{L}= 206.484 V$
Potential difference across the capacitor is given by,
${V}_{C}= I \times \dfrac {1}{\omega C}$
Substituting values in above equation we get,
${V}_{C}= 8.22 \times \dfrac {1} { 314 \times 60 \times {10}^{-6}}$
$\Rightarrow {V}_{C}= 8.22 \times 5.31 \times 10$
$\Rightarrow {V}_{C}= 436.5 V$
c) The average power transferred to the inductor is zero because the voltage leads current by ${\pi}/{2}$. The positive cycle cancels the negative cycle making zero average power of the inductor.
d) The average power transferred to the capacitor is zero because the voltage lags current by ${\pi}/{2}$. The positive cycle cancels the negative cycle making zero average power of the capacitor.
e) It is given that the resistance of the circuit is negligible. Thus, no power will be absorbed by the LC circuit over a cycle. So, the total power absorbed by the circuit is zero.

Note:
There is an alternate method to solve the first part of the question. Students can use the formula for impedance (Z) in terms of angular frequency, inductance and capacitance. Substitute the values in the formula and find the value of impedance. We know, impedance is nothing but the resistance. Now, use Ohm’s law giving a relationship between resistance, current and voltage. Substitute the values in the formula and obtain the value of current. This obtained value of the current will be rms value of current. Now, multiply this rms value with $\sqrt{2}$, this will give the amplitude of current.