Question
Question: A circuit consists of three batteries of emf \[{E_1} = 1{\text{V}}\], \({E_1} = 2{\text{V}}\) and \(...
A circuit consists of three batteries of emf E1=1V, E1=2V and E3=3V and internal resistances 1Ω, 2Ω and 1Ω respectively which are connected in parallel as shown in the figure. The potential difference between point P and Q is
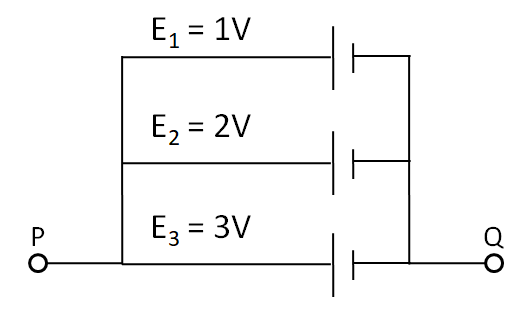
A. 1.0V
B. 2.0V
C. 2.2V
D. 3.0V
Solution
To solve this question, we need to use the formula for the equivalent emf of the batteries connected in parallel combination with each other. The batteries are connected in parallel combination across the point P and Q. Therefore the potential difference between the points P and Q will be equal to the equivalent emf of the batteries.
Formula used: The formulae used for solving this question are given by
ReqE=R1E1+R2E2+..........+RnEn
Req1=R11+R21+..........+Rn1
Here E is the equivalent emf of the parallel combination of the batteries of emfs E1, E2,…., En and internal resistances of R1, R2,….., Rn respectively. Also, Req is the equivalent internal resistance.
Complete step by step answer:
We know that the equivalent emf of a combination of batteries connected in parallel to each other is given by
ReqE=R1E1+R2E2+..........+RnEn (1)
According to the question, we have E1=1V, E2=2V, and E3=3V. Also, the internal resistances of these batteries are R1=1Ω, R2=2Ω, and R3=1Ω. Substituting these in (1) we get
ReqE=11+22+13
⇒ReqE=5 (2)
Also, since the internal resistances are connected in parallel combination with each other, the equivalent internal resistance of the combination is given by
Req1=R11+R21+..........+Rn1
Substituting R1=1Ω, R2=2Ω, and R3=1Ω in the above equation, we get
Req1=11+21+11
⇒Req1=25
Taking the reciprocal, we get
Req=52Ω
Substituting this in (2) we get
2/5E=5
⇒E=52×5=2V
So the equivalent emf of the given parallel combination of the batteries is equal to 2.0V. This means that the potential difference between the points P and Q is equal to 2.0V.
Hence, the correct answer is option B.
Note: There must be some drop across the equivalent internal resistance of the equivalent battery. This is because the circuit between points P and Q is not complete. So no current will flow through the equivalent battery, which means that the drop across the equivalent internal resistor will be equal to zero. Due to this we could take the potential difference is equal to the equivalent emf.
