Question

A circle with radius $\left| a \right|$ and centre on y-axis slides along it and a variable line though $\left( {a,0} \right)$ cuts the circle at points $P$ and $Q$. The region in which the point of intersection of tangents to the circle at points $P$ and $Q$ lies is represented by
A. ${y^2} \geqslant 4\left( {ax - {a^2}} \right)$
B. ${y^2} \leqslant 4\left( {ax - {a^2}} \right)$
C. $y \geqslant 4\left( {ax - {a^2}} \right)$
D. $y \leqslant 4\left( {ax - {a^2}} \right)$

Answer 1

Hint: First of all, consider the centre of the circle as a variable on the y-axis and find the equation of the circle. Then find the equation of chord of contact at points $P$ and $Q$. As the value of the y-coordinate of the centre of the circle is real, equate the value of discriminant to greater than or equal to zero.

Complete step-by-step answer:
Given radius of the circle is $\left| a \right|$
Let $\left( {0,\alpha } \right)$ be the centre of the circle as the centre lies on the y-axis.
We know that the equation of the circle with centre $\left( {h,k} \right)$ and radius $r$ is given by ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$.
So, the given circle equation is given by

$${\left( {x - 0} \right)^2} + {\left( {y - \alpha } \right)^2} = {\left( {\left| a \right|} \right)^2} \\\ {x^2} + {\left( {y - \alpha } \right)^2} = {a^2} \\\ {x^2} + {y^2} - 2\alpha y + {\alpha ^2} - {a^2} = 0 \\\ {x^2} + {y^2} - 2\alpha y + \left( {{\alpha ^2} - {a^2}} \right) = 0 \\\$$

Let $R\left( {h,k} \right)$ be the point of intersection of the tangents to the circle at points $P$ and $Q$ as shown in the below figure:

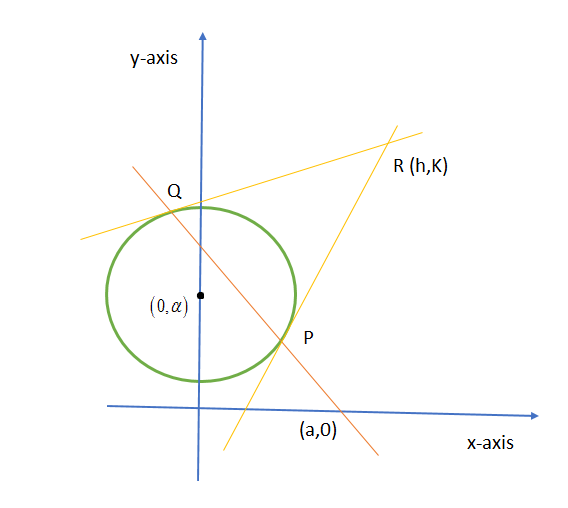
We know that the equation of chord of contact at $\left( {{x_1},{y_1}} \right)$ to the circle ${x^2} + {y^2} + 2gx + 2fy + c = 0$ is given by $x{x_1} + y{y_1} + g\left( {x + {x_1}} \right) + f\left( {y + {y_1}} \right) + c = 0$.
So, the equation of chord of contact i.e., equation of PQ is given by

$$xh + yk + 0\left( {x + h} \right) + \left( { - \alpha } \right)\left( {y + k} \right) + \left( {{\alpha ^2} - {a^2}} \right) = 0 \\\ xh + yk - \alpha \left( {y + k} \right) + \left( {{\alpha ^2} - {a^2}} \right) = 0 \\\$$

But this equation is passing through $\left( {a,0} \right)$. So, this point should satisfy the equation PQ.

$$ah + \left( 0 \right)k - \alpha \left( {0 + k} \right) + \left( {{\alpha ^2} - {a^2}} \right) = 0 \\\ ah - \alpha k + {\alpha ^2} - {a^2} = 0 \\\ {\alpha ^2} - \alpha k + ah - {a^2} = 0 \\\$$

We know that for the equation $a{x^2} + bx + c = 0$ if $x$ is a real value then its discriminant must be greater than or equal to zero i.e., ${b^2} - 4ac \geqslant 0$.
In the equation ${\alpha ^2} - \alpha k + ah - {a^2} = 0$ as $\alpha$ is a real since it is a variable and lies on y-axis its discriminant must be greater than equal to zero.
So, we have

$${\left( { - k} \right)^2} - 4\left( 1 \right)\left( {ah - {a^2}} \right) \geqslant 0 \\\ {k^2} - 4\left( {ah - {a^2}} \right) \geqslant 0 \\\ {k^2} \geqslant 4\left( {ah - {a^2}} \right) \\\$$

As we have to find the coordinates of $\left( {h,k} \right)$, we substitute $h = x$ and $k = y$, then we get
${y^2} \geqslant 4\left( {ax - {a^2}} \right)$
Thus, the correct option is A. ${y^2} \geqslant 4\left( {ax - {a^2}} \right)$

Note: The chord joining the points of contact of the two tangents to a conic drawn from a given point, outside it, is called the chord of contact. For the equation $a{x^2} + bx + c = 0$ if $x$ is a real value then its discriminant must be greater than or equal to zero i.e., ${b^2} - 4ac \geqslant 0$.