Question

A circle $S = 0$ is drawn with its Centre at $( - 1,1)$ so as to touch the circle ${x^2} + {y^2} - 4x + 6y - 3 = 0$ externally. Find the intercepts made by the circle $S = 0$ on the coordinate axes.

Answer 1

Here we have a center point of the circle and the circle equation. We have a formula for finding a radius. First, we will find the radius of the circle and we will substitute this value for the given equation. We will get the coordinate axis in the given equation.

Formula used:
Find the center of a circle
${r^2} = {(x - a)^2} + {(y - b)^2}$
Here $a$, $b$ is a center and r mean radius
Circle (-1,1)$= {(x + 1)^2} + {(y - 1)^2}$

Complete step by step solution:
First, we will find center for the given equation
${x^2} + {y^2} - 4x + 6y - 3 = 0$
Here $a = - 4,b = 6$
Now we have a center point $a,b$ is divided by $2$
$\therefore$ center point c1 $= (2, - 3)$
We will find r for the given equation
${x^2} - 4x + {y^2} + 6y - 3 = 0$
Then we take half value for $a,b$
${x^2} - 4x + {2^2} + {y^2} + 6y + {3^2} = 3 + {2^2} + {3^2}$
${(x - 2)^2} + {(y + 3)^2} = 3 + {2^2} + {3^2}$ (Here ${x^2} + 4x + {2^2}$ is formula of ${(x - 2)^2}$ and ${y^2} + 6y + {3^2}$ is formula of ${(y + 3)^2}$)
${(x - 2)^2} + {(y + 3)^2}$ is same as ${r^2}$
${r^2}$= $3 + {2^2} + {3^2}$, $r = \sqrt {3 + {2^2} + {3^2}}$, $r = \sqrt {16}$
$r = 4$

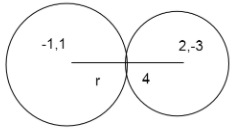
Now we find the $r + 4$ full radius
${r^2} = {(x - a)^2} + {(y - b)^2}$
$r = \sqrt {{{(x - a)}^2} + {{(y - b)}^2}}$
$r + 4 = \sqrt {{{(2 + 1)}^2} + {{(1 + 3)}^2}} ,r + 4 = \sqrt {{{(3)}^2} + {{(4)}^2}} ,r + 4 = \sqrt {9 + 16} ,r + 4 = \sqrt {25} ,r + 4 = 5$
So here $r = 1$
Circle $= {(x + 1)^2} + {(y - 1)^2} = 1$
${x^2} + 2x + 1 + {y^2} + 1 - 2y = 1$
Intercept = ${x^2} + {y^2} + 2x - 2y + 1,2\sqrt {{g^2} - c} = 0,2\sqrt {{f^2} - c} = 0$
Here $y = 0$ in given equation intercept
${x^2} + 2x + 1 = 0,x = 0$,
Here $x = 0$ in given equation intercept
${y^2} - 2y + 1 = 0$ , $y = 1$
So, intercept and $y$ axis $0$

Additional information:
Here we have a radius and the center point of one circle using this information we wind find what is the radius of the circle. But in case a given equation has a more efficient coefficient will give a different approach for this type of question.

Note:
In this question we have two circles. This question has a one center point for one circle. First, we will find another circle center point. This time we will have a clear understanding about the circle’s radius and the circles center points.
Because in this equation we have a diameter for the circle we will convert the radius of the circle.