Question

A circle passes through the point $( - 2,4)$ and touches the $y -$axis at the point $(0,2)$. Which one of the following equations can represent the diameter of the circle?
A. $2x - 3y + 10 = 0$
B. $4x + 5y - 6 = 0$
C. $5x + 2y + 4 = 0$
D. $3x + 4y - 3 = 0$

Answer 1

In this question, we will try to draw the figure. Then we are also given two points on the circle and then we will use the general equation of the circle with the radius $r$ and centre $(a,b)$
${(x - a)^2} + {(y - b)^2} = {r^2}$ and then we will be able to find the equation of diameter of the circle.

Complete step-by-step answer:

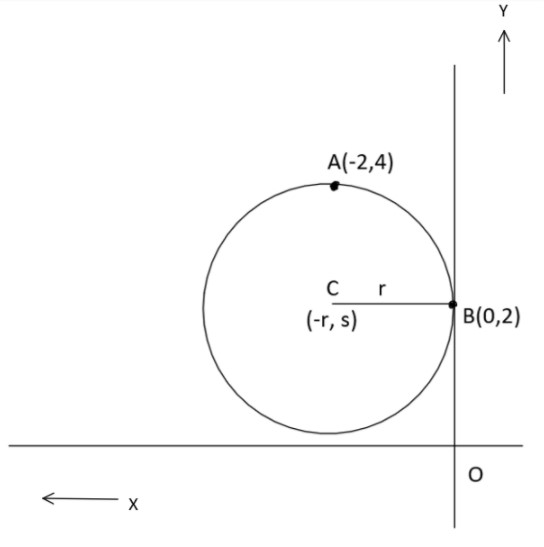
In this question, we are given that a circle passes through the point $( - 2,4)$ and touches the $y -$axis at the point $(0,2)$and we have to find an equation that can represent the diameter of the circle.
Now draw the figure by using the given information,
Let $C$ be the centre of the circle and $r$ be the radius of the circle.
As the circle lies in the second quadrant and the $y$ axis is the tangent to the circle at the point $B(0,2)$. Then the abscissa of the centre $C$ will be $r$, where $r$ is the radius of the circle.
Let $s$ be the ordinate of the point $C$.
So $C$ $= ( - r,s)$
We know that equation of the circle with the radius $r$ and centre $(a,b)$ and passes through $(x,y)$ is:
${(x - a)^2} + {(y - b)^2} = {r^2}$ $- - - - - - (1)$
Now we know that centre of the circle is at $C$ $= ( - r,s)$
And the radius is $r$, so for any point $(x,y)$ lying on the circle, equation of the circle using $(1)$ will be:
${(x - ( - r))^2} + {(y - s)^2} = {r^2}$
${(x + r)^2} + {(y - s)^2} = {r^2}$ $- - - - (2)$
Now we know that $B(0,2)$ passes through the circle. So it must satisfy the equation of the circle $(2)$
${(0 + r)^2} + {(2 - s)^2} = {r^2}$
${(r)^2} + {(2 - s)^2} = {r^2}$
Now after solving this we get:
$(2 - s) = 0$
So $s = 2$
Now we get ordinate of the point $C$
So $C$ becomes $( - r,2)$
Now putting $s = 2$ in (2), we get:
${(x + r)^2} + {(y - 2)^2} = {r^2}$ $- - - - - (3)$
We know that circle passes through the point $A$ $( - 2,4)$
So $A$ also satisfies the equation of the circle.
Putting value of $A$in (3), we get:
${( - 2 + r)^2} + {(4 - 2)^2} = {r^2}$
Now using the formula ${(a - b)^2} = {a^2} + {b^2} + 2ab$
$4 + {r^2} - 4r + 4 = {r^2}$
$8 - 4r = 0$
$r = 2$
So we get the radius of circle $r = 2$
And centre of the circle $C$ $= ( - 2,2)$
Now according to the question, we need to find the equation of diameter of the circle. Now We know that the diameter of the circle passes through the centre of the circle.
So, we can say that the diameter of the circle passes through $C$ $= ( - 2,2)$ so $C$ $= ( - 2,2)$ must satisfy the equation of the diameter and hence we can check the options which satisfy the equation of the diameter.
$2x - 3y + 10 = 0$
$2( - 2) - 3(2) + 10 = 0$
$- 4 - 6 + 10 = 0$
Which is correct.

So, the correct answer is “Option A”.

Note: In this question we have taken $r$ as the radius and it should be positive. And now as the circle lies in the second quadrant, so $x$ coordinate is negative there.