Question

A circle is inscribed in a $\Delta ABC$ with sides $AC$, $AB$ and $BC$ as $8cm$, $10cm$ and $12cm$. Find the length of $AD$, $BE$ and $CF$.

Answer 1

First we need to make the figure from the information given in the question. Then using the property of tangents that the tangents drawn from a point to a circle are equal in length, we can equate AD and AF, BD and BE, CE and CF. Then using the values of the sides given in the question with these equations, we can determine the respective lengths of the sides AD, BE and CF.

Complete step by step solution:
From the information given in the above question, we can draw the following figure.

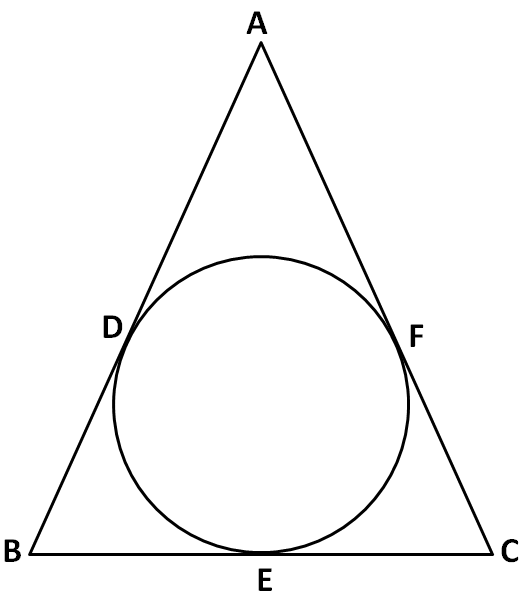
Now, we know that the lengths of the tangents from a point to a circle are equal. So from the above figure, we can say that
$\begin{aligned} & \Rightarrow BE=BD=x........(i) \\\ & \Rightarrow CF=CE=y........(ii) \\\ & \Rightarrow AF=AD=z........(iii) \\\ \end{aligned}$
So now we can have the following figure

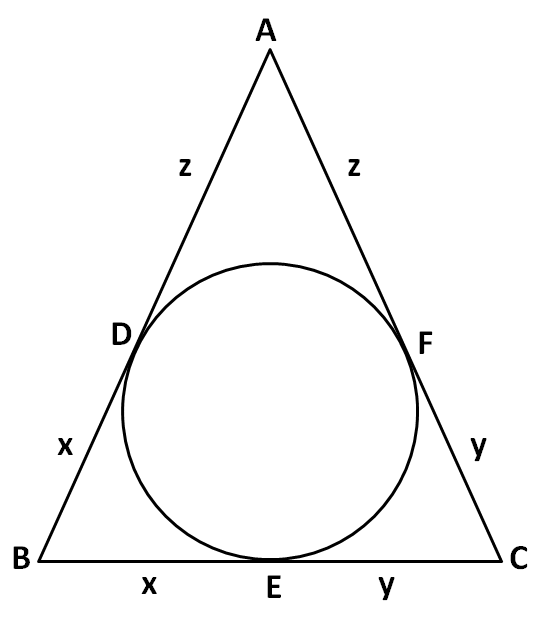
Now, according to the question, the sides of the triangle AC, AB and AC are $8cm$, $10cm$ and $12cm$ respectively. So from the above figure we have
$\begin{aligned} & \Rightarrow y+z=8cm........(iv) \\\ & \Rightarrow x+z=10cm........(v) \\\ & \Rightarrow x+y=12cm........(vi) \\\ \end{aligned}$
Subtracting (iv) from (v) we have
$\begin{aligned} & \Rightarrow x+z-\left( y+z \right)=10-8 \\\ & \Rightarrow x-y=2cm.........(vii) \\\ \end{aligned}$
Adding (vi) and (vii) we get
$\begin{aligned} & \Rightarrow x+y+\left( x-y \right)=12+2 \\\ & \Rightarrow 2x=14 \\\ & \Rightarrow x=7cm \\\ \end{aligned}$
Putting this in (v) we get
$\begin{aligned} & \Rightarrow 7+z=10 \\\ & \Rightarrow z=10-7 \\\ & \Rightarrow z=3cm \\\ \end{aligned}$
Putting this in (iv) we get
$\begin{aligned} & \Rightarrow y+3=8 \\\ & \Rightarrow y=8-3 \\\ & \Rightarrow y=5cm \\\ \end{aligned}$
Therefore, the side AD is
$\begin{aligned} & \Rightarrow AD=z \\\ & \Rightarrow AD=3cm \\\ \end{aligned}$
The side BE is

& \Rightarrow BE=x \\\ & \Rightarrow BE=7cm \\\ \end{aligned}$$ And the side CF is $$\begin{aligned} & \Rightarrow CF=y \\\ & \Rightarrow CF=5cm \\\ \end{aligned}$$ **Hence, the sides AB, BE and CF are $3cm$, $7cm$ and $5cm$ respectively.** **Note:** In this question, we were not given the figure corresponding to the question. So we had to assume the locations of the points D, E and F on the triangle. For simplicity, we took these adjacent to the vertices A, B, and C respectively. But if you take them opposite to the respective vertices, then AD, BE and CF will become the altitudes and you will need to use the Pythagoras theorem for calculating the lengths of the same.