Question

A circle is drawn with origin as the center passes through $\left( \dfrac{13}{2},0 \right)$. The point does not lie in the interior of the circle.
A. $\left( \dfrac{-3}{4},1 \right)$
B. $\left( 2,\dfrac{7}{3} \right)$
C. $\left( 5,\dfrac{-1}{2} \right)$
D. $\left( -6,\dfrac{5}{2} \right)$

Answer 1

First of all, we need to make the equation in the form of ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ then we can start solving the problem by recalling the conditions for a point to lie inside, outside or on the circle i.e., if $S\equiv 0$is the equation of the circle and $\left( {{x}_{1}},{{y}_{1}} \right)$ is any point and if ${{S}_{11}}=0$ then the point lies on the circle, if ${{S}_{11}}<0$ then the point lies inside the circle, if ${{S}_{11}}>0$, then the point lies outside the circle.. We then substitute each point which is given in the option in the obtained equation of the circle and check whether it is satisfying the condition or not to get the required answer.

Complete step by step answer:
According to the problem, we have given a circle passing through a point $\left( \dfrac{13}{2},0 \right)$ and we need to find the points which do not lie on the interior of the circle. Before we going to the problem, we need to know the conditions that is if $S\equiv 0$ is the equation of the circle and $\left( {{x}_{1}},{{y}_{1}} \right)$ is any point.
If ${{S}_{11}}=0$ then the point lies on the circle,
If ${{S}_{11}}<0$ then the point lies inside the circle,
If ${{S}_{11}}>0$, then the point lies outside the circle.

First of all, we need to find the equation of circle for that we need to find the radius that is
The circle which is passing through $\left( \dfrac{13}{2},0 \right)$ the radius of circle is
$r=\sqrt{{{\left( 6.5-0 \right)}^{2}}+{{\left( 0-0 \right)}^{2}}}$
By simplifying this we get:
$r=\sqrt{{{\left( 6.5 \right)}^{2}}}$
By removing the square, we get:
$r=6.5$
For understanding this clearly, Figure is given below

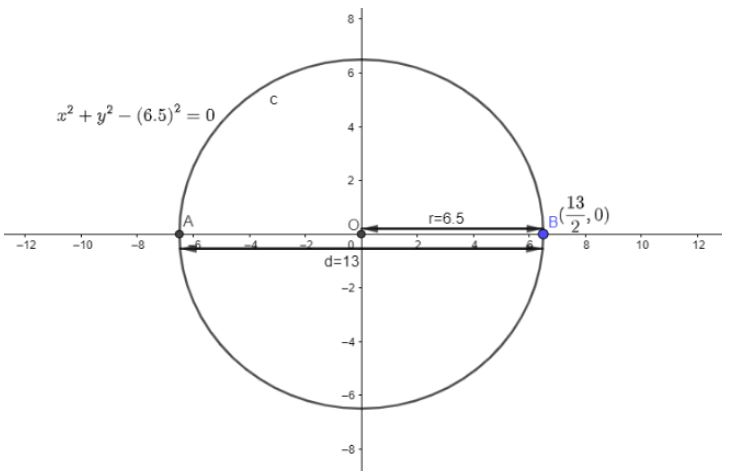
In the above figure the radius is 6.5. We know the general equation of circle that is,
${{x}^{2}}+{{y}^{2}}={{r}^{2}}$
By substituting the value of radius, we get;
${{x}^{2}}+{{y}^{2}}={{\left( 6.5 \right)}^{2}}$
By rearranging the term, we get:
${{x}^{2}}+{{y}^{2}}-{{\left( 6.5 \right)}^{2}}=0---(1)$

Now, we will see one by one options to get the required answer. To get the answer we will check if ${{S}_{11}}<0$ then the point lies inside the circle, otherwise it will outside the circle if we consider the first option that is $\left( \dfrac{-3}{4},1 \right)$ when we substitute this value on equation (1) we get:
$\Rightarrow {{\left( \dfrac{-3}{4} \right)}^{2}}+1-{{\left( 6.5 \right)}^{2}}$
By simplifying this we get:
$\Rightarrow -39<0$
That means points lie on the inside the circle

Similarly, we can check other option that is in case of option B that is $\left( 2,\dfrac{7}{3} \right)$ we get:
By substituting one equation (1) we get:
$\Rightarrow {{\left( 2 \right)}^{2}}+{{\left( \dfrac{7}{3} \right)}^{2}}-{{\left( 6.5 \right)}^{2}}$
By simplifying this we get:
$\Rightarrow 4+\left( \dfrac{49}{9} \right)-{{\left( 6.5 \right)}^{2}}$
By solving we get the value as $-32.89<0$
Hence, the point lies inside the circle.

Similarly, option C that is $\left( 5,\dfrac{-1}{2} \right)$ and substituting this we get:
$\Rightarrow {{\left( 5 \right)}^{2}}+{{\left( \dfrac{-1}{2} \right)}^{2}}-{{\left( 6.5 \right)}^{2}}$
By simplifying this we get:
$\Rightarrow 25+\left( \dfrac{1}{4} \right)-{{\left( 6.5 \right)}^{2}}$
By cross multiply and simplification, we get:
$\Rightarrow -17<0$
Hence, the point lies inside the circle.

Now, we go for option D that is $\left( -6,\dfrac{5}{2} \right)$ we get:
$\Rightarrow {{\left( -6 \right)}^{2}}+{{\left( \dfrac{5}{2} \right)}^{2}}-{{\left( 6.5 \right)}^{2}}$
By simplifying this we get:
$\Rightarrow 36+\left( \dfrac{25}{4} \right)-{{\left( 6.5 \right)}^{2}}$
By solving this we will get the answer as zero since, rest of the three option A, B and D is negative sign that’s why those three points are inside the circle but condition is given outside the circle hence, option D is selected in this problem, even the answer which we get the answer in option D as zero.

Therefore, the correct option is “option D”.

Note: We should not confuse $S<0$ for lying outside the circle which is the most common mistake done by the students. The conditions we have just discussed for a point lying inside, outside or on the circle is valid for all conics not only for the circle. We can also solve this problem by checking whether the distance from the centre of the circle to that point is greater than the radius of the circle in order to present outside the circle. Similarly, we can expect problems to find the total number of tangents drawn from that point on to the circle.