Question
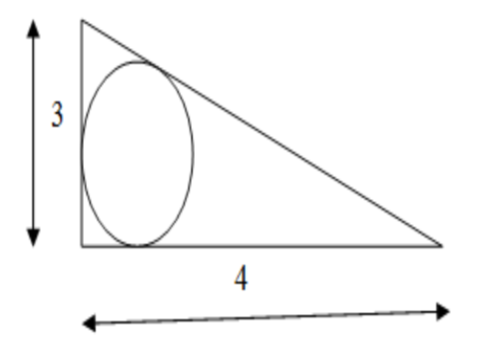
Question: A circle is drawn in a triangular board as shown in the figure if a ball is thrown to the board, ...
A circle is drawn in a triangular board as shown in the figure
if a ball is thrown to the board, then find the probability of the ball that collide in the interior of the circle.
Solution
We denote the vertices of the triangle as A, B, C where ∠B is the right angle. We are given AB=3, BC=4 and we find AC using the Pythagoras theorem. We find the area of the triangle as n(T)=21×AB×BC. We denote the center of the circle as O and join AO, BO, CO. We use the fact that the area of the triangle ABC is the sum of the area of the triangle AOB say, the area of triangle BOC and the area of the triangle AOC say to find the radius of the circle r. We find the area of the circle as n(C)=πr2 and the required probability as n(T)n(C).
Complete step-by-step solution:
We know from definition of probability of hitting target with region A with area of interior n(A)and S is region under observation with area of interior n(S) then the probability of hitting or striking in the region A is P(A)=n(S)n(A).
We are given the question that a circle is drawn on the triangular board. We are asked to find the probability that of colliding a ball in the interior of the circle. So the striking area is the interior of the circle say $n\left( C \right)$ and the total area is the area of the interior of the triangle say $n(T)$. So the probability of the ball colliding inside the circle is $P=\dfrac{n\left( C \right)}{n\left( T \right)}$.
We denote the vertices of the given triangles as A,B,C where $\angle B$ is the right angle. We are given AB=3 and BC=5 units. We use the Pythagoras theorem and find the length of hypotenuse AC as $AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{{{3}^{2}}+{{5}^{2}}}=5$units. The area of the triangle is $n\left( T \right)=\dfrac{1}{2}\times AB\times BC=\dfrac{1}{2}\times 4\times 3=6$ square units.
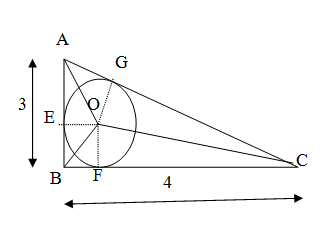
We denote the center of the circle as O and join AO, BO, CO. We join the center O and denote the point of contact of the circle with sides AB, BC, AC as E, F, G respectively. We know that the radius of a circle is always perpendicular to its tangent. So we have OE, OF, OG are perpendicular to the sides AB, BC, AC respectively. They are also the radii of the circle. So let us have OE=OF=OG=r.
We see that the area of the triangle ABC is the sum of area of the triangle AOB say n(T1), area of triangle BOC n(T2) and the area of the triangle AOC say n(T3). So we have
