Question

A circle is described whose center is the vertex and whose diameter is three-quarters of the latus rectum of a parabola. Prove that the common chord of the circle and parabola bisects the distance between the vertex and the focus.

Answer 1

Hint: Draw a suitable diagram with the help of given information to visualize the problem accurately. Latus rectum of parabola ${{y}^{2}}=4ax$ will lie at x = a. Common chord of circle and parabola will be given by relation ${{s}_{1}}-{{s}_{2}}=0$, where ${{s}_{1}}$ is the equation of one curve and ${{s}_{2}}$is of second. Mid-point of two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ on a line is given as
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$

Complete step-by-step answer:
Let us suppose the equation of parabola be ${{y}^{2}}=4ax$, whose vertex is (o, o) and is symmetric about x-axis and length of the latus rectum is 4a as per the definition of parabola.
So, diagram of parabola is given as

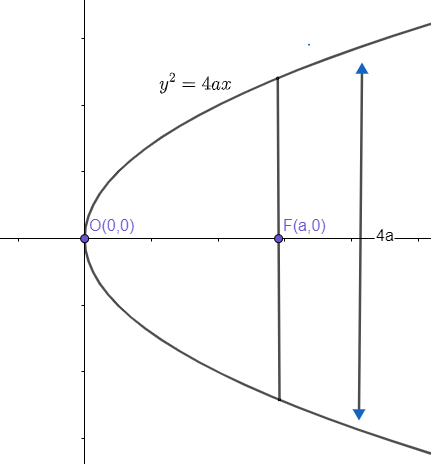
Where (a, o) is the focus of the parabola.
Now, a circle is drawn with center at the vertex i.e. at (o, o) and diameter of $\dfrac{3}{4}th$ of the latus rectum i.e. diameter $=\dfrac{3}{4}\left( 4a \right)=3a$. Hence, the radius of the circle would be given as $\left( \dfrac{3a}{2} \right)$ as the diameter is just double of radius.
Now, we know the standard equation of the circle is given by equation
${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}$ ………………..(i)
Where, $\left( {{x}_{1}},{{y}_{1}} \right)$is centre and r is the radius of the circle.
So, equation of the circle with (0, 0) as centre and radius as $\dfrac{3a}{2}$ will be given as
${{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{\left( \dfrac{3a}{2} \right)}^{2}}$
${{x}^{2}}+{{y}^{2}}=\dfrac{9{{a}^{2}}}{4}$ ……………(ii)
Now, we have to prove that the common chord of the circle and parabola bisects the distance between vertex and focus.
So, diagram with the help of above information is given as:

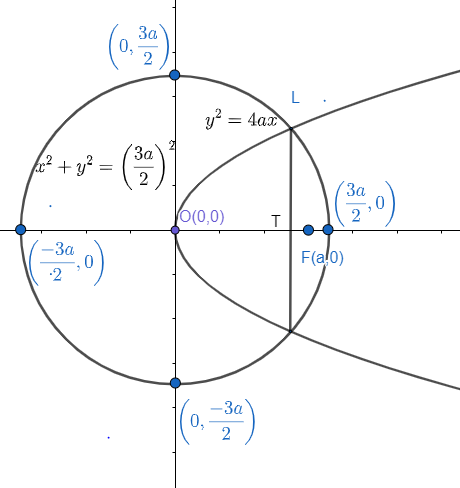
Where line L is the common chord of parabola and circle, as given in the diagram and F(a, 0) is the focus of the parabola.
Now, we know the common chord of two conics is given by equation
${{s}_{1}}-{{s}_{2}}=0$ ……………..(iii)
Where, ${{s}_{1}},{{s}_{2}}$ are the equations of the conics.
So, both the equations of circle and parabola are given as
$\begin{aligned} & \to {{x}^{2}}+{{y}^{2}}=\dfrac{9{{a}^{2}}}{4},{{y}^{2}}=4ax \\\ & \to {{s}_{1}}:{{x}^{2}}+{{y}^{2}}-\dfrac{9{{a}^{2}}}{4}=0,{{s}_{2}}={{y}^{2}}-4ax=0 \\\ \end{aligned}$
Now, from the equation (iii), we can get equation of common chord as
$\begin{aligned} & \to \left( {{x}^{2}}+{{y}^{2}}-\dfrac{9{{a}^{2}}}{4} \right)-\left( {{y}^{2}}-4ax \right)=0 \\\ & \to {{x}^{2}}+{{y}^{2}}-\dfrac{9{{a}^{2}}}{4}-{{y}^{2}}+4ax=0 \\\ & {{x}^{2}}-\dfrac{9{{a}^{2}}}{4}+4ax=0,\dfrac{4{{x}^{2}}-9{{a}^{2}}+16ax}{4}=0, \\\ \end{aligned}$
$4{{x}^{2}}+16ax-9{{a}^{2}}=0$……………(iv)
Now, as the above equation is quadratic in ‘x’, so, we can get values of ‘x’ using the quadratic formula to get roots of any quadratic equation
$A{{x}^{2}}+Bx+C=0$ is given as
$x=\dfrac{-B\pm \sqrt{{{B}^{2}}-4AC}}{2A}$ ………………. (v)
Hence, we get values of ‘x’ from equation (iv) and (v) as
$\begin{aligned} & \to x=\dfrac{-16a\pm \sqrt{{{\left( 16a \right)}^{2}}-4\times 4\times \left( -9{{a}^{2}} \right)}}{2\times 4} \\\ & \to x=\dfrac{-16a\pm \sqrt{256{{a}^{2}}+144{{a}^{2}}}}{8} \\\ & \to x=\dfrac{-16a\pm \sqrt{400{{a}^{2}}}}{8} \\\ & \to x=\dfrac{-16a\pm 20a}{8} \\\ \end{aligned}$
So, we can get two values f ‘x’ as
$\begin{aligned} & x=\dfrac{-16a+20a}{8},x=\dfrac{-16a-20a}{8} \\\ & x=\dfrac{4a}{8},x=\dfrac{-36a}{8} \\\ & x=\dfrac{a}{2},x=\dfrac{-9a}{2} \\\ \end{aligned}$
Now, from the diagram, we can observe the common chord of the curves will lie in positive x-direction only so, we can ignore $x=\dfrac{-9a}{2}$, which is lying in direction of negative direction of x-axis.
So, $x=\dfrac{a}{2}$is the equation of the common chord of the given curves.
So, the point T, (where the common chord is meeting at x-axis) is given as $\left( \dfrac{a}{2},o \right)$.
Now, we know mid-point of any two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$on a line, is given as $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
So, mid-point of focus F(a, o) and vertex 0(o, o) can be given as
$\left( \dfrac{a+o}{2},\dfrac{o+o}{2} \right),\left( \dfrac{a}{2},o \right)$
Hence, the point $T\left( \dfrac{a}{2},o \right)$ is representing the mid-point of the focus and vertex of the parabola.
So, the common chord is bisecting the focus and vertex.
Hence, the given statement is proved.

Note: One may solve the given equations of circle and parabola to get the equation of common chord. As ${{s}_{1}}-{{s}_{2}}=0$ is also representing the solution of both the equations as well. So, both the approaches are the same. So, try to use the formula ${{s}_{1}}-{{s}_{2}}=0$ to get the common chord to get rid of solving both the equations.
Fundamental concepts of parabola and ellipse should be very clear to solve these kinds of questions.
Another approach for the question would be to suppose the equation of common chord as
y = mx + c and try to solve it with the circle and parabola both. And hence, get the intersection points to calculate the equation of the common chord passing through both of the curves. But it will be a longer approach than given in solution. So, always try to solve these questions by visualizing the calculation part as well.