Question

A circle, having radius “r” has a line charge distribution over its circumference having linear charge density $\lambda = {\lambda _0}{\cos ^2}\theta$. Calculate the total electric charge residing on the circumference of the circle. $\left[ {\int\limits_0^{2\pi } {{{\cos }^2}\theta d\theta = \pi } } \right]$

Answer 1

Hint: The differential charge element for length $dl$ from circumference in terms of $d\theta$ is $dl = rd\theta$

Formula Used:
1. $Q = \int {dq}$ over the entire domain. …… (a)
2. Charge density, $\lambda = \dfrac{{dq}}{{dl}}$ …… (b)
3. Differential element, $dl = rd\theta$ …… (c)
4. Given required integral to use, $\int\limits_0^{2\pi } {{{\cos }^2}\theta d\theta = \pi }$ …… (d)

Complete step by step answer:

Given,
charge density $\lambda = {\lambda _0}{\cos ^2}\theta$ …… (1)
radius of circle $= r$

Step 1 of 6:

Figure 1 shows the relationship between variables of integrand $d\theta$ and $dl$

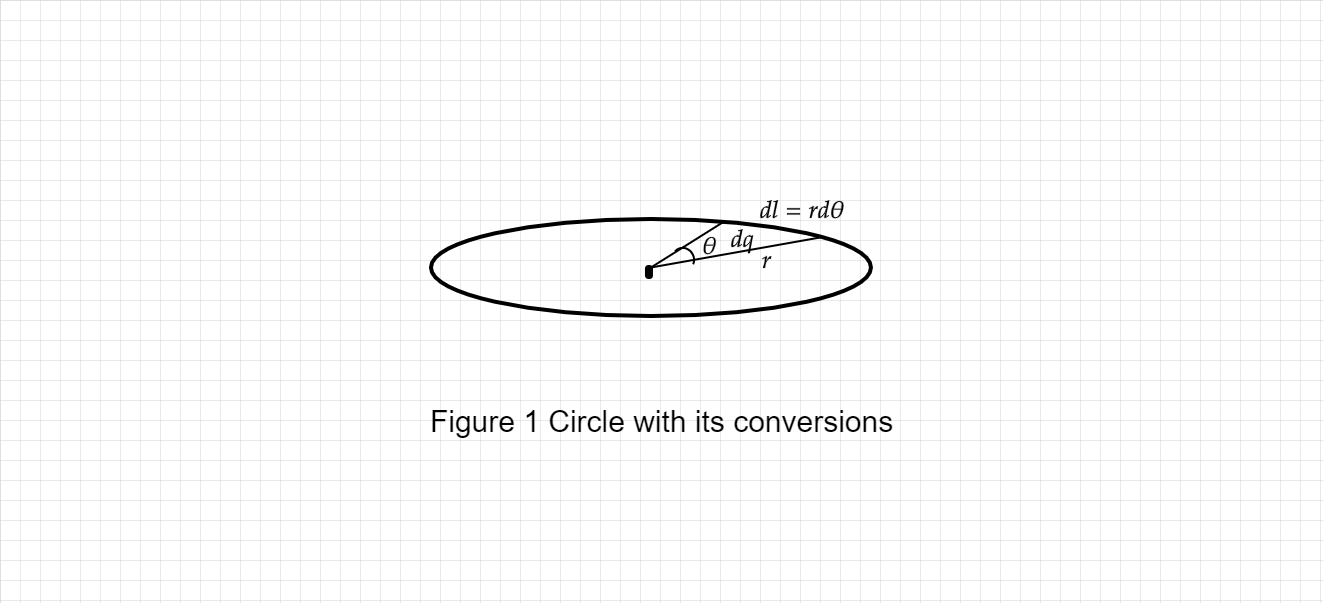
Step 2 of 6:

Substituting values from equation (c) in equation (b) we get
$\lambda = \dfrac{{dq}}{{rd\theta }}$ where $dl = rd\theta$
$\Rightarrow dq = \lambda dl = \lambda rd\theta$ …… (2)

Step 3 of 6:

Putting value from equation (2) in equation (a) gives us
$Q = \int {dq}$ $\Rightarrow Q = \int {\lambda rd\theta }$ where $Q$is total charge distribution on given domain …… (3)

Step 4 of 6:

Substituting equation (1) in equation (3) we get
$Q = \int {{\lambda _0}r{{\cos }^2}\theta d\theta }$ where ${\lambda _0}$ and $r$ are constants …… (4)

Step 5 of 6:

Moving constants out of integration and supplying integration limit 0 to 2$\pi$ we get-
$Q = {\lambda _0}r\int\limits_0^{2\pi } {{{\cos }^2}\theta d\theta }$ …… (5)

Step 6 of 6:

Substituting value from equation (d) in equation (5) we get $Q = \pi {\lambda _0}r$

Correct Answer:

$Q = \pi {\lambda _0}r$

Additional Information:
Integrals like equations (d) are very useful in solving problems with circular symmetric axis. Above problem is solved in the polar coordinate system. Similarly, if surface or volume charge density is given then, one should focus on change of variable in integration so that it transforms into some known integral form. For example, equation (d)

Note: We should always try to solve our problem considering the given hints from the question itself. Here, integration was already provided which saved a lot of time.