Question

A circle has the same Centre as an ellipse and passes through the foci ${F_1}$ and ${F_2}$ of the ellipse, such that the two curves intersect in four points. Let $P$ be any one of their points of intersection. If the major axis of the ellipse is $17$ and the area of triangle $P{F_1}{F_2}$ is $30$, then the distance between the foci is
(A) $13$
(B) $10$
(C) $11$
(D) None of these

Answer 1

We will first find the radius of the given circle in terms of major axis and eccentricity. Then we will equate this radius to the given value of radius to obtain an equation in terms of $x$ , $y$ , major axis and minor axis. With the help of this equation, we will find the value of $y$ , and then we will use this value of $y$ to find the area of the triangle $P{F_1}{F_2}$ . Equating this to the given area will give the value of major axis and minor axis, using these values in the required equation will give the distance between the foci.

Complete step-by-step solution:
We know that the equation of ellipse is
$\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1 - - - (1)$

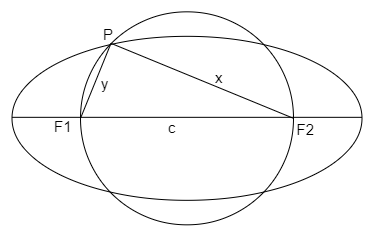
Also, it is given in the question that the centre of the circle is same as that of the ellipse and it passes through the foci of the ellipse, therefore, the radius of the circle is:
$r = ae$
Now we will put the value of $e$ in the above equation. So,
$r = a\sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}}$
$\Rightarrow r = \sqrt {{a^2} - {b^2}}$
Now replacing $r$ with $\sqrt {{x^2} + {y^2}}$ , we get,
$\sqrt {{x^2} + {y^2}} = \sqrt {{a^2} - {b^2}}$
So, the equation of circle becomes,
${x^2} + {y^2} = {a^2} - {b^2}$
$\Rightarrow {x^2} = {a^2} - {b^2} - {y^2} - - - (2)$
Substituting the value of ${x^2}$ from this equation into equation $(1)$ , we get,
$\dfrac{{{a^2} - {b^2} - {y^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$
$\Rightarrow 1 + \dfrac{{{y^2}}}{{{b^2}}} - \dfrac{{{b^2} + {y^2}}}{{{a^2}}} = 1$
On further simplification it becomes,
$\Rightarrow \dfrac{{{y^2}}}{{{b^2}}} = \dfrac{{{b^2} + {y^2}}}{{{a^2}}}$
On cross-multiplication,
$\Rightarrow {y^2}{a^2} = {b^2}\left( {{b^2} + {y^2}} \right)$
On rearranging it becomes,
$\left( {{a^2} - {b^2}} \right){y^2} = {b^4}$
$\Rightarrow {y^2} = \dfrac{{{b^4}}}{{\left( {{a^2} - {b^2}} \right)}}$
On taking square-root of both sides,
$\Rightarrow |y| = \dfrac{{{b^2}}}{{\sqrt {{a^2} - {b^2}} }}$
Now, area of triangle is $= \dfrac{1}{2}|y|\left( {{F_1}{F_2}} \right)$
$= \dfrac{1}{2}|y|\left( {2ae} \right)$
On putting the values of $r$ and $ae$ we get,
Area of triangle $= \dfrac{1}{2} \times \dfrac{{{b^2}}}{{\sqrt {{a^2} - {b^2}} }} \times 2\sqrt {{a^2} - {b^2}}$
$= {b^2}$
But it is given that the area of the triangle is $30$ . So,
${b^2} = 30$
Also, it is given that $2a = 17$
Now we know that:
${F_1}{F_2} = 2ae$
$\Rightarrow {F_1}{F_2} = 2\sqrt {{a^2} - {b^2}}$
Now, putting the values of ${a^2}$ and ${b^2}$ , we get,
$\Rightarrow {F_1}{F_2} = 2\sqrt {\left( {\dfrac{{{{17}^2}}}{{{2^2}}} - 30} \right)}$
$\Rightarrow {F_1}{F_2} = 2\sqrt {\left( {\dfrac{{289 - 120}}{4}} \right)}$
On further simplification it becomes,
$\Rightarrow {F_1}{F_2} = \sqrt {\left( {169} \right)}$
$\Rightarrow {F_1}{F_2} = 13$

Note: One of the major problems that one can have in these types of questions is that they get confused in the formula for eccentricity. Whether it is $e = \sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}}$ or $e = \sqrt {1 - \dfrac{{{a^2}}}{{{b^2}}}}$ . Actually, it is $e = \sqrt {1 - \dfrac{{{{{\text{(minor - axis)}}}^2}}}{{{\text{(major - axis)}^2}}}}$ .