Question

A circle cuts two perpendicular lines so that each intercept is of given length. The locus of the centre of the circle is a conic whose eccentricity is
A. 1
B. $\dfrac{1}{{\sqrt 2 }}$
C. $\sqrt 2$
D. None of the above.

Answer 1

A locus is a set of points which satisfy certain geometric conditions. To simplify the question, we can assume that x-axis and y-axis are the perpendicular lines. Choose a coordinate system that will make computations and equations as simple as possible i.e. general equation of circle.
That is,
${x^2} + {y^2} + 2gx + 2fy + c = 0$ represent the equation of circle with centre $( - g, - f)$ and radius equal to ${a^2} = {g^2} + {f^2} - c$.
To find the locus, we need to write the given conditions in a mathematical form involving the coordinates ‘x’ and ‘y’.

Complete step by step solution:
Equation of circle is ${x^2} + {y^2} + 2gx + 2fy + c = 0$.
Let x-axis and y-axis are two perpendicular lines and let the constant intercept be $a$ and $b$ in x-axis and y-axis respectively.

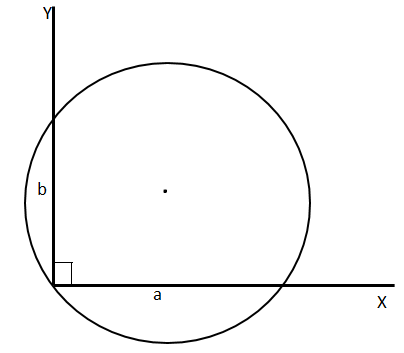
We know that the ‘x’ Intercept length is
$2\sqrt {{g^2} - c} = a$
$\sqrt {{g^2} - c} = \dfrac{a}{2}$
Squaring on both sides we have,
${g^2} - c = {\left( {\dfrac{a}{2}} \right)^2}$
$\Rightarrow {g^2} - c = \dfrac{{{a^2}}}{4}{\text{ }} - - - (1)$
We know that the ‘y’ Intercept length is
$2\sqrt {{f^2} - c} = b$
$\sqrt {{f^2} - c} = \dfrac{b}{2}$
Squaring on both sides we have,
${f^2} - c = {\left( {\dfrac{b}{2}} \right)^2}$
$\Rightarrow {f^2} - c = \dfrac{{{b^2}}}{4}{\text{ }} - - - - (2)$
Add the equation (1) and equation (2),
${g^2} - {f^2} = \dfrac{{{a^2}}}{4} - \dfrac{{{b^2}}}{4}$
$\Rightarrow {g^2} - {f^2} = \dfrac{{{a^2} - {b^2}}}{4}$
We know that, centre of the circle is $( - g, - f)$.
To find the locus, replace the coordinate of circle with ‘x’ and ‘y’,
$\Rightarrow {x^2} - {y^2} = \dfrac{{{a^2} - {b^2}}}{4}$
Let assume $\dfrac{{{a^2} - {b^2}}}{4} = {m^2}$ to simplify the expression,
$\Rightarrow {x^2} - {y^2} = {m^2}$
$\Rightarrow \dfrac{{{x^2}}}{{{m^2}}} - \dfrac{{{y^2}}}{{{m^2}}} = \dfrac{{{m^2}}}{{{m^2}}}$
$\Rightarrow \dfrac{{{x^2}}}{{{m^2}}} - \dfrac{{{y^2}}}{{{m^2}}} = 1$
General equation of hyperbola is $\Rightarrow \dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$, where ‘a’ and ‘b’ are major and minor axes length,
Therefore, above equation is Hyperbola and, on comparing we get that$a = m$ and $b = m$
And as we know that,
The eccentricity of hyperbola is $e = \sqrt {1 + \dfrac{{{a^2}}}{{{b^2}}}}$,
On substituting the value of ‘a’ and ‘b’,
$e = \sqrt {1 + \dfrac{{{m^2}}}{{{m^2}}}}$
$e = \sqrt {1 + 1}$
$\Rightarrow e = \sqrt 2$

Hence the eccentricity is $\sqrt 2$.

Hence, the required answer is (c).

Note: Here we got the locus which is a hyperbola. There can be any type of conic section (ellipse parabola) which we can get according to the given question and we need to have knowledge about the standard form of equation of the curve to recognize.