Question

A circle C whose radius is 1 unit touches the x – axis at point A. Then centre Q of C lies in the first quadrant. The tangent from the origin O to the circle touches it at T and a point P lies on it such that$\Delta {\text{OAP}}$ is a right – angled triangle at A and its perimeter is 8 units.
The equation of tangent OT is
(1) 3y = 4x
(2) ${\text{x - }}\sqrt 2 {\text{y = 0}}$
(3) ${\text{y - }}\sqrt 3 {\text{x = 0}}$
(4) none of these

Answer 1

Hint: To solve this question, we will draw a figure according to the question. We will use Pythagoras theorem for the $\Delta {\text{OAP}}$ which is ${\text{O}}{{\text{P}}^2}{\text{ = O}}{{\text{A}}^2}{\text{ + P}}{{\text{A}}^2}$ and also use the distance formula $\sqrt {{{({{\text{x}}_2}{\text{ - }}{{\text{x}}_1})}^2}{\text{ + (}}{{\text{y}}_2}{\text{ - }}{{\text{y}}_1}{)^2}}$ . Also, we will use the equation of straight line $({\text{y - }}{{\text{y}}_1}){\text{ = }}\dfrac{{{{\text{y}}_2}{\text{ - }}{{\text{y}}_1}}}{{{{\text{x}}_2}{\text{ - }}{{\text{x}}_1}}}({\text{x - }}{{\text{x}}_1})$ to find the equation of tangent OT.

Complete step-by-step answer:
Now, the circle touches the x – axis at point A. Also, the centre of circle Q lies in the first quadrant. The radius of the circle is 1 unit. OT is the tangent from origin O to circle which touches the circle at point T. Point P lies on the tangent OT. So, the figure is

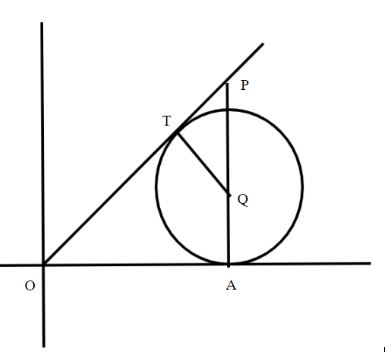
Now, the radius of the circle is 1 unit. So, from the figure, QA = 1 unit and QT = 1 unit. Let the coordinates of centre Q be (h,1). Therefore, the coordinates of point A is (h,0). Let coordinates of point P be (h, k).
Now, the tangent is perpendicular to the radius at the point of contact. So, we get $\angle {\text{OAP = 9}}{{\text{0}}^0}$ and $\angle {\text{QTP = 9}}{{\text{0}}^0}$.
Now, we will apply Pythagoras theorem in $\Delta {\text{OAP}}$,
${\text{O}}{{\text{P}}^2}{\text{ = O}}{{\text{A}}^2}{\text{ + A}}{{\text{P}}^2}$ … (1)
Now, AP = $\sqrt {{{({{\text{x}}_2}{\text{ - }}{{\text{x}}_1})}^2}{\text{ + (}}{{\text{y}}_2}{\text{ - }}{{\text{y}}_1}{)^2}}$ (By distance formula)
Therefore, AP = $\sqrt {{{({\text{h - h}})}^2}{\text{ + (k - 0}}{)^2}}$ = k units.
OA = $\sqrt {{{({\text{h - 0}})}^2}{\text{ + (0 - 0}}{)^2}}$ = h units.
So, from equation (1), we get
${\text{O}}{{\text{P}}^2}{\text{ = }}{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}$
${\text{OP = }}\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}}$
Also, in $\Delta {\text{PQT}}$ applying Pythagoras theorem, we get
${\text{P}}{{\text{Q}}^2}{\text{ = Q}}{{\text{T}}^2}{\text{ + P}}{{\text{T}}^2}$
PQ = $\sqrt {{{({\text{h - h)}}}^2}{\text{ + (k - 1}}{{\text{)}}^2}}$ = (k – 1) units
Therefore, ${\text{P}}{{\text{T}}^2}{\text{ = P}}{{\text{Q}}^2}{\text{ - T}}{{\text{Q}}^2}$
${\text{P}}{{\text{T}}^2}{\text{ = (k - 1}}{{\text{)}}^2}{\text{ - 1}}$
${\text{PT = }}\sqrt {{{{\text{(k - 1)}}}^2}{\text{ - 1}}}$
Also, from an external the length of tangents to circle are equal to each other. So, from point O, OT and OA are tangents of the circle. Therefore, OT = OA = h units.
Now, OP = OT + TP
Putting values, we get
$\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{ = h + }}\sqrt {{{({\text{k - 1)}}}^2}{\text{ - 1}}}$
Squaring both sides, we get
${(\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{)}}^2}{\text{ = (h + }}\sqrt {{{({\text{k - 1)}}}^2}{\text{ - 1}}} {)^2}$
${{\text{h}}^2}{\text{ + }}{{\text{k}}^2}{\text{ = }}{{\text{h}}^2}{\text{ + (k - 1}}{{\text{)}}^2}{\text{ - 1 + 2h}}\sqrt {{{({\text{k - 1)}}}^2}{\text{ - 1}}}$
On simplification the above term, we get
${\text{k = }}\dfrac{{{\text{2}}{{\text{h}}^2}}}{{{{\text{h}}^2}{\text{ - 1}}}}$ … (2)
Now, perimeter of $\Delta {\text{OAP}}$ = 8 units
OA + OP + AP = 8
Putting values in the above expression, we get
${\text{h + k + }}\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{ = 8}}$
We can write the above expression as,
$\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{ = 8 - (h + k)}}$
Squaring both sides, we get
${(\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}} {\text{)}}^2}{\text{ = (8 - (h + k)}}{{\text{)}}^2}$
${{\text{h}}^2}{\text{ + }}{{\text{k}}^2}{\text{ = 64 + }}{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}{\text{ + 2kh - 16(h + k) }}$
On Simplifying the above expression, we get
${\text{hk - 8(h + k) + 32 = 0}}$
Putting value of k from the equation (2), we get
${\text{h}}\left( {\dfrac{{{\text{2}}{{\text{h}}^2}}}{{{{\text{h}}^2}{\text{ - 1}}}}} \right){\text{ - 8(h + }}\dfrac{{{\text{2}}{{\text{h}}^2}}}{{{{\text{h}}^2}{\text{ - 1}}}}){\text{ }} + {\text{ }}32{\text{ = 0}}$
$2{{\text{h}}^3}{\text{ - 8(h(}}{{\text{h}}^2}{\text{ - 1) + 2}}{{\text{h}}^2}){\text{ + 32(}}{{\text{h}}^2}{\text{ - 1) = 0}}$
On simplification, we get
$3{{\text{h}}^3}{\text{ - 8}}{{\text{h}}^2}{\text{ - 4h + 16 = 0}}$
Now, the factors of the above cubic equation are 2,2 and $- \dfrac{4}{3}$
Now, as the circle lies in the first quadrant, so we take h = 2. So, putting the value of h in equation (2), we get
${\text{k = }}\dfrac{{2{{(2)}^2}}}{{{{{\text{(2)}}}^2}{\text{ - 1}}}}$
$\Rightarrow$ ${\text{k = }}\dfrac{8}{3}$
So, the coordinates of point P are (h, k) i.e. (2, $\dfrac{8}{3}$). Also, the coordinates of origin O are (0,0). So, by using formula to find equation of straight line $({\text{y - }}{{\text{y}}_1}){\text{ = }}\dfrac{{{{\text{y}}_2}{\text{ - }}{{\text{y}}_1}}}{{{{\text{x}}_2}{\text{ - }}{{\text{x}}_1}}}({\text{x - }}{{\text{x}}_1})$, we get
$({\text{y - 0}}){\text{ = }}\dfrac{{\dfrac{8}{3}{\text{ - 0}}}}{{{\text{2 - 0}}}}({\text{x - 0}})$
${\text{y = }}\dfrac{4}{3}{\text{x}}$
3y = 4x
So, the equation of tangent OT is 3y = 4x. So, option (1) is correct.

Note: When we come up with such types of questions, we have to first draw a figure according to the question. Such questions can’t be solved without a figure. So, a figure is necessary to solve the given problem. Also, we have used some properties of tangent to circle. All the properties should be used carefully to solve the question. Pythagoras theorem is also used to solve this question. To find the equation to tangent, the formula to find the equation of a straight line is used.