Question

A circle C whose radius is 1 unit touches the x – axis at point A. the centre of C lies in the first quadrant. The tangent from origin O to the circle touches it at T and a point P lies on it such that triangle OAP is a right angled triangle at A and it’s perimeter is 8 units.
The length of OP is
(a) $\dfrac{1}{2}$
(b) $\dfrac{4}{3}$
(c)$\dfrac{5}{3}$
(d) none of these

Answer 1

Firstly we will find the length of PQ in terms of $\alpha$, then we will find the equation of perpendicular on tangent which is radius of circle and obtain the equation in terms of h and $\alpha$. Then, we will find the perimeter of the circle which is equal to 8 and will substitute the value of $\alpha$ in terms of h in equation perpendicular and will then obtain the positive value of $\alpha$ and hence will obtain the length of PQ.

Complete step-by-step answer:

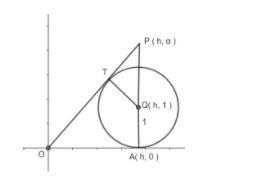
Let, from the figure we can see that length PA is $\alpha$ then, length of PQ will be $\alpha -1$.
Now, we know that the equation of tangent will be ax – by = 0, where ( b, a ) is the point where circle and tangent meets and tangent passes through origin.
So, here ( b, a ) is ( h, $\alpha$), then
Equation of tangent will be $\alpha$x - hy = 0
We know that, radius of the circle is perpendicular to the tangent drawn at the circle.
So, length of perpendicular on tangent = 1, as radius of circle is 1 unit.
Now, using formula for length of perpendicular, which is
$\left| \dfrac{h\alpha -h}{\sqrt{{{\alpha }^{2}}+{{h}^{2}}}} \right|=1$
Squaring both sides we get
$\dfrac{{{(h\alpha -h)}^{2}}}{{{\alpha }^{2}}+{{h}^{2}}}=1$
Using, cross multiplication, we get
${{h}^{2}}{{\alpha }^{2}}+{{h}^{2}}-2{{h}^{2}}\alpha ={{\alpha }^{2}}+{{h}^{2}}$
On simplifying we get
${{h}^{2}}\alpha -2{{h}^{2}}=\alpha$
Or, $\alpha =\dfrac{2{{h}^{2}}}{{{h}^{2}}-1}$
Or, $\alpha -1=\dfrac{2{{h}^{2}}}{{{h}^{2}}-1}-1$
$\alpha -1=\dfrac{{{h}^{2}}+1}{{{h}^{2}}-1}$ as, PQ is $\alpha -1$.
Now, Perimeter of Triangle will be $h\text{ }+\alpha +\sqrt{{{h}^{2}}+{{\alpha }^{2}}}$, as OA = h, PA =$\alpha$ and OP = $\sqrt{{{h}^{2}}+{{\alpha }^{2}}}$
Also, given in question that perimeter is equal to 8.
So, $h\text{ }+\alpha +\sqrt{{{h}^{2}}+{{\alpha }^{2}}}=8$
On re – writing, we get
$\sqrt{{{h}^{2}}+{{\alpha }^{2}}}=8-h-\alpha$
Putting $\alpha =\dfrac{2{{h}^{2}}}{{{h}^{2}}-1}$in $\sqrt{{{h}^{2}}+{{\alpha }^{2}}}=8-h-\alpha$, we egt
$\sqrt{{{h}^{2}}+{{\left( \dfrac{2{{h}^{2}}}{{{h}^{2}}-1} \right)}^{2}}}=8-h-\dfrac{2{{h}^{2}}}{{{h}^{2}}-1}$
Squaring both sides we get
${{h}^{2}}+{{\left( \dfrac{2{{h}^{2}}}{{{h}^{2}}-1} \right)}^{2}}=64+{{h}^{2}}+{{\left( \dfrac{2{{h}^{2}}}{{{h}^{2}}-1} \right)}^{2}}-16h+2h\left( \dfrac{2{{h}^{2}}}{{{h}^{2}}-1} \right)-16\dfrac{2{{h}^{2}}}{{{h}^{2}}-1}$
On simplifying we get
$64-16h+2h\left( \dfrac{2{{h}^{2}}}{{{h}^{2}}-1} \right)-16\dfrac{2{{h}^{2}}}{{{h}^{2}}-1}=0$
$64-16h+\left( \dfrac{4{{h}^{3}}-32{{h}^{2}}}{{{h}^{2}}-1} \right)=0$
$\left( \dfrac{64{{h}^{2}}-64-16{{h}^{3}}-16h+4{{h}^{3}}-32{{h}^{2}}}{{{h}^{2}}-1} \right)=0$
Or, $3{{h}^{3}}-8{{h}^{2}}-4h+16=0$
${{(h-2)}^{2}}(3h+4)=0$
So, $h=2,-\dfrac{4}{3}$
As, length cannot be negative, so h = 2
Putting, h = 2 in $PQ=\alpha -1=\dfrac{{{h}^{2}}+1}{{{h}^{2}}-1}$, we get
$PQ=\alpha -1=\dfrac{{{2}^{2}}+1}{{{2}^{2}}-1}$
$PQ=\alpha -1=\dfrac{5}{3}$units.

So, the correct answer is “Option C”.

Note: To solve these types of questions one must have a pictorial understanding of the question at a good level as it decreases the chances of mistakes and also makes questions even easier to solve. Try to avoid making calculation mistakes and always mention units in the final answer.