Question
Question: A circle and a square (wire frame) each of mass \(m\) are arranged as shown in the diagram. The diam...
A circle and a square (wire frame) each of mass m are arranged as shown in the diagram. The diameter of the circle and the edge of the square are 2R each. Find the moment of inertia of this configuration about XX.
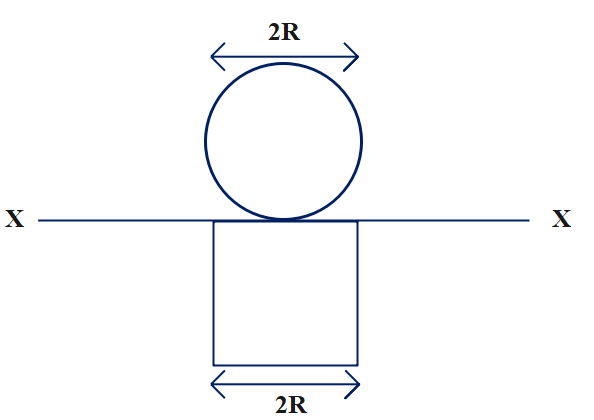
A.617mR2B.611mR2C.619mR2D.613mR2
Solution
Moment of inertia is the property of a body to resist any angular acceleration. It is mathematically given as the sum of the product of the masses of every particle with the square of the distances from the chosen axis of rotation. It is also known as the angular mass or rotational inertia of the given object.
Formula: I=mk2
Complete answer:
Moment of inertia is the resistance offered by any object against rotational acceleration. We know that the moment of inertia depends on the density of the given material, the axis of rotation and the dimensions of the given body, i.e. the shape and the size of the body. We also know that, the moment of inertia depends primarily on the mass of the object and its distance from the axis of rotation
Let us consider the given circle of mass of the to be m, and R its radius. Similarly, the mass of each rod in the square is m and length 2R
Then the moment of inertia I experienced by the circle during a rotation along its own axis is given by I=mk2, where kis the radius of gyration. If we consider the component of the inertia along the x and y axis, is given as I=mR2+mR2
I=2mR2. Now the inertia at the centre of the circle from the parallel axis theorem Ic=2mR2+mR2
Since one of the rod of AD the square lies on the axis it has no inertia, whereas the inertia due to each of the perpendicular rod AB, DC is given a 12m(2R)2. And the inertia due to the final rod BC is given as 4m(2R)2+0.
Then the total inertia due to the square is given as Is=2×12m(2R)2+mR2.
Then the total inertia along XX is given as I=Ic+Is=2mR2+mR2+2×12m(2R)2+mR2.
⟹I=2mR2+32mR2+2mR2
⟹I=619mR2
Hence the correct answer is option C.619mR2
Note:
The radius of gyration k has a unique value for each object. Thus it is useful to remember the value of k or I for some simple objects. Also the question might look complex, but it can be solved easily, if the formulas and the gyration k are known.
