Question

A chunk of conductor with a hollowed-out core has charge placed on it until its potential (relative to infinity) is φ0. What is the potential inside the core?

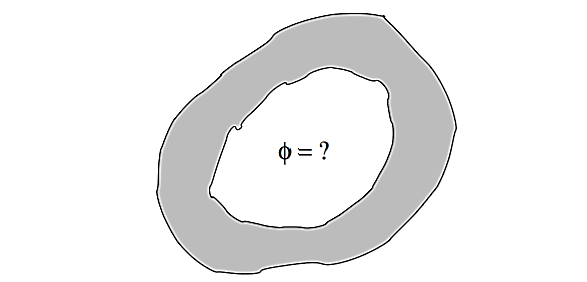
A) θ
B) ∞
C) ϕ0
D) none of these

Answer 1

Inside the conductor is hollow, the net electric field inside is zero.

Complete step by step solution:
Given a conductor with hollowed out core having potential ϕ0. Inside the conductor is hollow, the net electric field inside is zero. It means the difference in potential inside and on the surface is zero. So, the potential inside the core = potential on the conductor = ϕ0 is a solution that satisfies the boundary condition, and it obviously satisfies Laplace’s equation (since ϕ0 is a constant).

**Correct Answer: C) ϕ 0 **

Note: Laplace’s equation, second-order partial differential equation widely useful in physics because its solutions R (known as harmonic functions) occur in problems of electrical, magnetic, and gravitational potentials, of steady-state temperatures, and of hydrodynamics. The equation was discovered by the French mathematician and astronomer Pierre-Simon Laplace.