Question

A chord of a parabola cuts the axis of the parabola at O. The feet of the perpendiculars from P and P’ on the axis are M and M’ respectively. If V is the vertex then VM, VO, VM’ are
(a) A.P
(b) G.P
(c) H.P
(d) AP, GP

Answer 1

To solve this question we will first take an equation of a parabola and then try to draw its figure using the given points in the question. Any point P on the parabola is of the form $P\left( a{{t}^{2}},2at \right)$ where t varies. We will use that the slope of the line with endpoints is given by $\dfrac{{{y}_{1}}-{{y}_{2}}}{{{x}_{1}}-{{x}_{2}}}$ where $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the endpoints.

Complete step-by-step answer:
To solve this question, we will first consider some parabola. To do that let us define a parabola and some examples. The parabola is the locus of points in that plane that are equidistant from both the directrix and the focus. Another description of a parabola is a conic section, created from the intersection of a right circular conical surface and a plane parallel to another plane that is tangential to the conical surface. The examples of the standard parabola are:
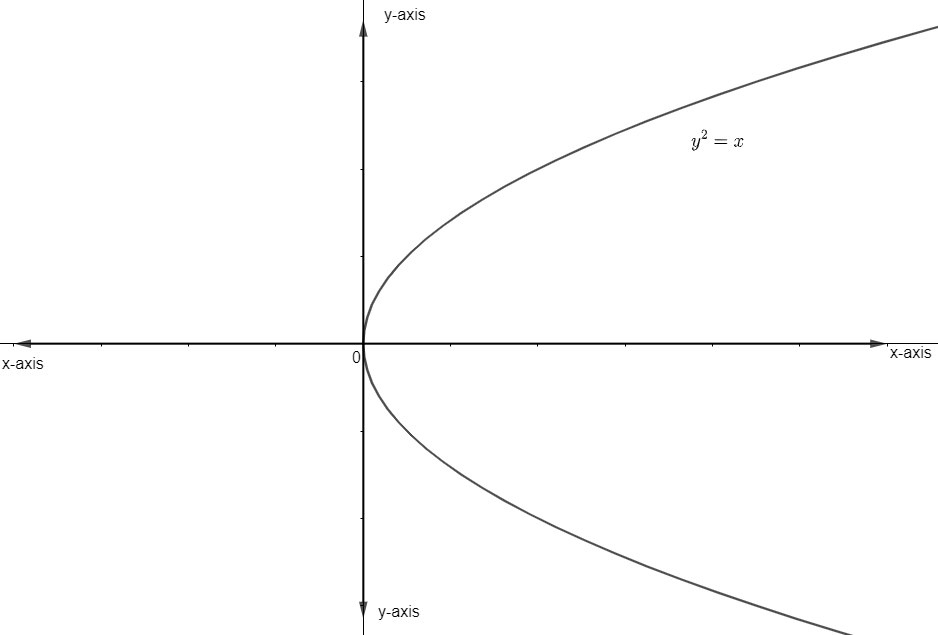
$\left( I \right){{y}^{2}}=x$
It is drawn as

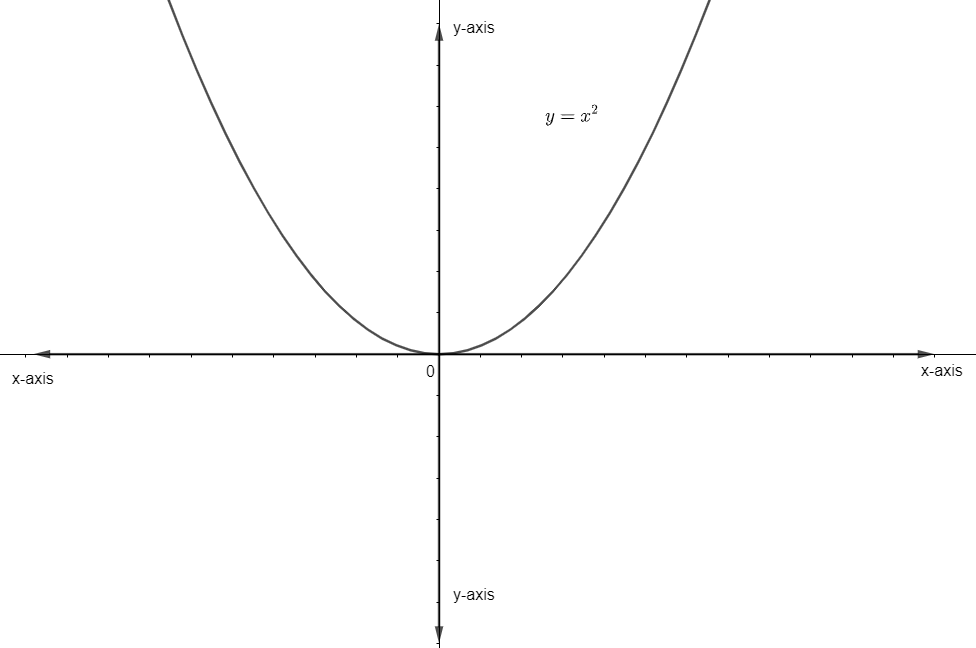
$\left( II \right)y={{x}^{2}}$
It is drawn as

From these, let the parabola be ${{y}^{2}}=4ax$

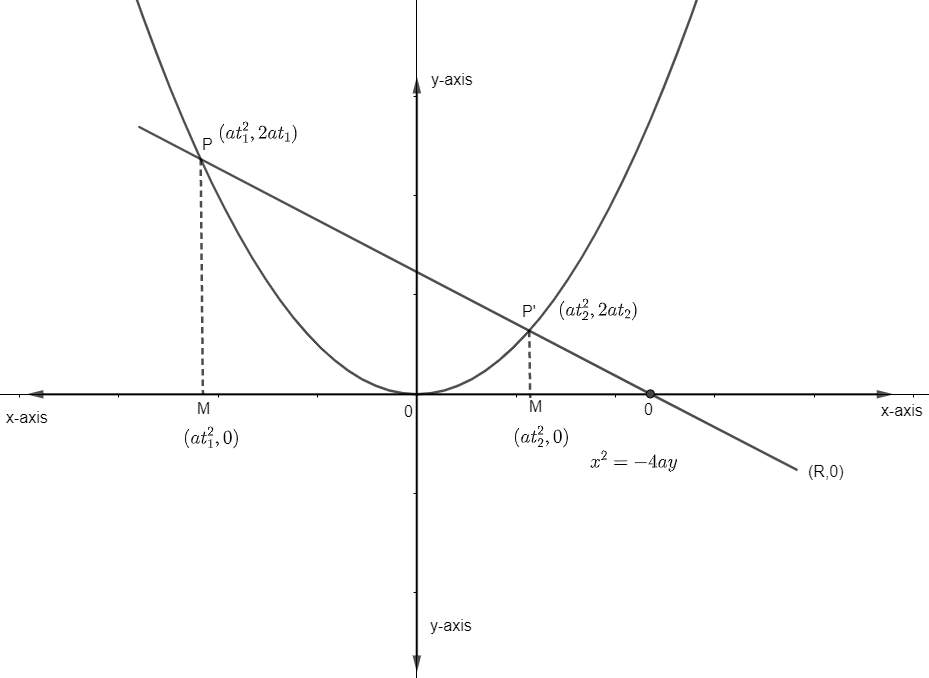
Let the vertex of parabola be V = (0, 0). The chord PP’ cuts x-axis at 0 and let it be (R, 0).
$\Rightarrow VO=R$
Let $P=\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ be the coordinates of the point P. This is so as any point on the parabola is of the form $P=\left( a{{t}^{2}},2at \right)$ where t varies. Then the foot of the perpendicular on the axis is $M=\left( a{{t}_{1}}^{2},0 \right)$ (as visible by the diagram) and similarly for ${{P}^{'}}=\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ the foot of the perpendicular is ${{M}^{'}}\left( a{{t}_{2}}^{2},0 \right)$ the coordinate of the point (0, 0). The slope of the line having endpoints as $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $\dfrac{{{y}_{1}}-{{y}_{2}}}{{{x}_{1}}-{{x}_{2}}}.$ Then for PO, the slope is given by the slope of $PO=\dfrac{2a{{t}_{1}}}{a{{t}_{1}}^{2}-R}.$
Similarly, the slope of P’O is given by (using the above formula) the slope of ${{P}^{'}}O=\dfrac{-2a{{t}_{2}}}{R-a{{t}_{2}}^{2}}.$
Now because PO and P’O are forming the same line, so then the slopes are equal.
The slope of PO = Slope of P’O
$\Rightarrow \dfrac{2a{{t}_{1}}}{a{{t}_{1}}^{2}-R}=\dfrac{-2a{{t}_{2}}}{R-a{{t}_{2}}^{2}}$
On cross multiplying, we get,
$\Rightarrow 2a{{t}_{1}}\left( R-a{{t}_{2}}^{2} \right)=-2a{{t}_{2}}\left( a{{t}_{1}}^{2}-R \right)$
$\Rightarrow {{t}_{1}}R-a{{t}_{2}}^{2}{{t}_{1}}=-a{{t}_{1}}^{2}{{t}_{2}}+{{t}_{2}}R$
$\Rightarrow R\left( {{t}_{1}}-{{t}_{2}} \right)=a{{t}_{2}}^{2}{{t}_{1}}-a{{t}_{1}}^{2}{{t}_{2}}$
$\Rightarrow R=\dfrac{a{{t}_{1}}{{t}_{2}}\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( {{t}_{1}}-{{t}_{2}} \right)}$
$\Rightarrow R=-a{{t}_{1}}{{t}_{2}}$
Hence, the value of R is $-a{{t}_{1}}{{t}_{2}}.$
So, we have,
$VO=R$
$VM=a{{t}_{1}}^{2}$
$V{{M}^{'}}=a{{t}_{2}}^{2}$
$\Rightarrow V{{O}^{2}}={{R}^{2}}$
Substituting $R=-a{{t}_{1}}{{t}_{2}}$
$\Rightarrow V{{O}^{2}}={{R}^{2}}$
$\Rightarrow V{{O}^{2}}={{\left( -a{{t}_{1}}{{t}_{2}} \right)}^{2}}$
$\Rightarrow V{{O}^{2}}={{a}^{2}}{{t}_{1}}^{2}{{t}_{2}}^{2}$
$\Rightarrow V{{O}^{2}}=a{{t}_{1}}^{2}a{{t}_{2}}^{2}$
$\Rightarrow V{{O}^{2}}=VM.V{{M}^{'}}$
$\Rightarrow {{\left( VO \right)}^{2}}=VM.V{{M}^{'}}$
Hence, VM, VO, VM’ are in GP.

So, the correct answer is “Option (c)”.

Note: When three numbers a, b and c are in GP, then they can be written as $ac={{b}^{2}}.$ Here, we have obtained the answer as ${{\left( VO \right)}^{2}}=VM.V{{M}^{'}}$ the number using the above stated theory are in GP.